Once the attention-based quantizer formation is completed, a prioritization protocol should be used to choose the allocation of bits among competing quantizers up to availability limit ![]() , at any given time of the transmission, where: (i) Intra-quantizer prioritization simply follows
embedded zerotree coding [6]; and (ii)
bit allocation among competing quantizers
, at any given time of the transmission, where: (i) Intra-quantizer prioritization simply follows
embedded zerotree coding [6]; and (ii)
bit allocation among competing quantizers
![]() follows bit allocation analysis by finding the efficient combination of allocations
follows bit allocation analysis by finding the efficient combination of allocations ![]() up to the bit consumption limitation.
up to the bit consumption limitation.
Intra-quantizer prioritization by zerotree coding provides substantial coding gains over the first-order entropy for significance maps. Zerotree coding
predicts insignificance across scales and spatio-temporal orientations using a model that is easy for most sequences to satisfy.
The zerotree approach can isolate interesting non-zero details by immediately eliminating large insignificant 3D regions from consideration.
At very low bit rates, where the probability of an insignificant coefficient must be high and thus, the significant threshold must also be large, expecting the occurrence of zerotrees and encoding significance maps using zerotree coding is reasonable for every competing quantizer ![]() : If it is observed that a parent is insignificant with respect to the threshold, a zerotree is expected regardless of the correlation between squares of parents (coefficients) and squares of children.
Hence we have that differences in quantization costs
: If it is observed that a parent is insignificant with respect to the threshold, a zerotree is expected regardless of the correlation between squares of parents (coefficients) and squares of children.
Hence we have that differences in quantization costs ![]() for competing quantizers
for competing quantizers ![]() are not relevant, at extremely low bit rates, in determining the technological possibilities of the transmission problem.
The basic allocation processes
are not relevant, at extremely low bit rates, in determining the technological possibilities of the transmission problem.
The basic allocation processes
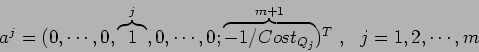
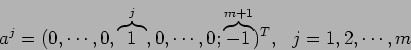
In the maximization of ![]() with respect to
with respect to ![]() over the set of allocation processes
over the set of allocation processes ![]() at any given time
at any given time ![]() , we have that
, we have that
From Chapter 1 in Reference [10], it follows that, within a rational approach for progressive transmission, the gross profit per bit ![]() for any quantizer
for any quantizer ![]() at any time
at any time ![]() can have the form of its expected increase in utility per coding bit
can have the form of its expected increase in utility per coding bit
![]() as given by Proposition 3 in [11], with
as given by Proposition 3 in [11], with ![]() denoting the maximum availability of bit resources for quantizer
denoting the maximum availability of bit resources for quantizer ![]() at time
at time ![]() and
and ![]() being the number of bits in
being the number of bits in ![]() . For example,
. For example, ![]() may be a fixed number of sorting and refinement bit streams from the
may be a fixed number of sorting and refinement bit streams from the ![]() intra-quantizer prioritization which follows the embedded zerotree coding scheme.
Reference [11] demonstrates that this definition avoids certain forms of behavioral inconsistency within a rational approach which first states some general principles that the solution of this problem must obey and then derives the solution that satisfies exactly the principles.
intra-quantizer prioritization which follows the embedded zerotree coding scheme.
Reference [11] demonstrates that this definition avoids certain forms of behavioral inconsistency within a rational approach which first states some general principles that the solution of this problem must obey and then derives the solution that satisfies exactly the principles.
In any case, the theory of bit allocation analysis allows to achieve efficient allocations which may be descriptive of reality at any given time of the progressive transmission, since the profit vector can change its value over time to give a good predictor of target saliency for humans performing visual search and detection tasks at any given bit rate. An example is presented in the following section of experimental results.
One possible use of our results would be for a video codec to possess several alternative definitions of a profit vector ![]() in such a way that a user of the system may choose the appropriate strategy for computing vector
in such a way that a user of the system may choose the appropriate strategy for computing vector ![]() at different bit rates to the application of interest.
at different bit rates to the application of interest.
For example, at extremely low bit rates (e.g., up to 10 kbps) a profit vector
Thus, in bit allocation analysis, the system makes a choice from the set of efficient allocations at any given time by using the appropriate strategy for computing the profit vector. It may allow to attend to different parameters of interest at different bit rates within the same spatial locations.