Siguiente: Experimentos y Resultados Anterior: Mochila Clásica Arriba: Mochila Clásica

Implementación de FANS

La aplicación de FANS a este problema es relativamente directa y simple. Las soluciones se representan mediante vectores binarios, lo cual permite utilizar un operador de modificación $k$-BitFlip, que simplemente cambia el valor de $k$ posiciones seleccionados al azar.

La valoración difusa representa la noción de ``Aceptabilidad'' con la siguiente idea: aquellas soluciones que mejoran el costo actual tienen un grado de aceptabilidad mayor que aquellas que lo empeoran. Aquellas soluciones cuyo costo sea peor que cierto umbral, no se consideran como aceptables.

Siendo $f$ la función objetivo, $s$ la solución actual, $\hat s = \mathcal{O}(s)$ una nueva solución, y $\beta < f(s)$ el límite para lo que se considera aceptable, la función de pertenencia siguiente modeliza el comportamiento deseado:

$\mu(\hat s, s) = \begin{cases} 0& \text{si $f(\hat s) < \beta$}\\ \frac{(f(\h... ...\beta \leq f(\hat s) \leq f(s)$}\\ 1& \text{si $f(\hat s) > f(s)$} \end{cases}$

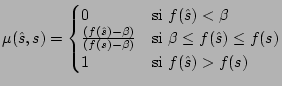
En dicho trabajo se utilizó $\beta = f(s) * 0.95$.

Para adaptar el operador de modificación, el administrador de operación cambia el valor del parámetro $k$. Cada vez que se ejecuta el administrador, el valor de $k$ se reemplaza por un nuevo valor entero $\hat k$, elegido aleatoriamente en el rango $[1,2*k]$. Además, si $\hat k > n/10$, donde $n$ es el tamaño de la instancia, entonces $\hat k = n/10$.

Para el administrador de vecindario, se utilizó un Esquema de Agrupamiento basado en la Calidad [7], el cual tiene en cuenta el grado de aceptabilidad de las soluciones para decidir cual debe ser devuelta. Los parámetros utilizados fueron $R=5\vert S=3\vert T=1$ y $maxTrials = 25$

El administrador intenta generar $R$ soluciones ``Aceptables'' mediante el operador $\mathcal{O}$ utilizando a lo sumo un número máximo de intentos $maxTrials$. Luego, las soluciones obtenidas se agrupan en $S$ conjuntos difusos teniendo en cuenta los grados de aceptabilidad, y finalmente se devuelve 1 solución. El lector puede considerar el segundo paso como un proceso de clustering sencillo.

Los $S=3$ conjuntos difusos o clusters se representan mediante funciones de pertenencia triangulares solapadas, cuyos extremos se ajustan al rango $[\lambda, 1.0]$, siendo $\lambda = 0.98$ el mínimo nivel que necesita una solución para ser considerada como aceptable. Los conjuntos representan los términos Baja, Media, Alta para la variable lingüística Calidad. Al final del proceso se devuelve una única solución ($T=1$). La regla de selección es:

Retornar alguna solución de las de
máxima calidad disponible.

Si no existe ninguna solución con calidad suficiente, se generara una condición de excepción ya que no fue posible encontrar ningún vecino aceptable con los elementos disponibles.