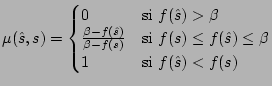
En el método de Recocido Simulado, la aceptación de soluciones esta gobernada por un parámetro denominado ``Temperatura''. Las soluciones que mejoran el costo actual siempre son aceptadas. Aquellas que lo empeoran también pueden ser aceptadas con cierta probabilidad, que será alta al inicio de la ejecución. A medida que la búsqueda progresa, la temperatura disminuye, decrementando entonces la probabilidad de aceptación de soluciones peores. Hacia el final de la ejecución, solo las soluciones mejores son aceptadas.
Para reflejar este comportamiento mediante la valoración difusa, se puede utilizar la siguiente definición de ``Aceptabilidad'':
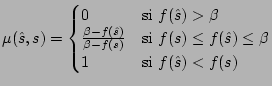
donde ![]() es la función objetivo,
es la función objetivo, ![]() es la solución actual y
es la solución actual y
![]() es una solución del vecindario operativo.
es una solución del vecindario operativo.
El valor ![]() representa el límite para lo que se considera aceptable.
Este valor es clave ya que en última instancia determina que soluciones
pertenecen o no al vecindario semántico. Si se define
representa el límite para lo que se considera aceptable.
Este valor es clave ya que en última instancia determina que soluciones
pertenecen o no al vecindario semántico. Si se define ![]() como una
función
como una
función
![]() donde
donde ![]() es un parámetro que represente por ejemplo
el número actual de iteraciones, el límite de deterioro aceptable puede
ser reducido a medida que la búsqueda progresa. Hacia el final de la
ejecución, solo aquellas soluciones mejores que la actual serán tenidas en
cuenta. Un ejemplo para la función
es un parámetro que represente por ejemplo
el número actual de iteraciones, el límite de deterioro aceptable puede
ser reducido a medida que la búsqueda progresa. Hacia el final de la
ejecución, solo aquellas soluciones mejores que la actual serán tenidas en
cuenta. Un ejemplo para la función ![]() es:
es:
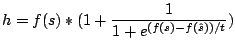 |
(3) |
En términos más generales, ![]() representan el umbral de aceptabilidad y por lo tanto,
su variación está reflejando una clase de algoritmos más amplia, los algoritmos de umbral.
representan el umbral de aceptabilidad y por lo tanto,
su variación está reflejando una clase de algoritmos más amplia, los algoritmos de umbral.