Fitting with Stochastic Gradient Descent

Stochastic gradient descent (SGD) is a general method for optimizing parameters given the partial derivatives of the error function relative to the parameters [Bottou 1998].

$$\nabla_{c,i} \ \textrm{Err}_R(D,\beta,\sigma^2) = \frac{\par... ...d \beta) - \log p(\beta \mid \sigma^2)\right)\nonumber\\ [6pt]$$

For logistic regression, the error function is a sum of contributions of the individual training cases and parameters, with the derivatives distributing through to individual cases.

The derivatives distribute through the cases for the data log likelihood:

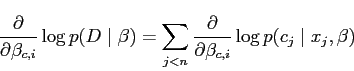$$\frac{\partial} {\partial \beta_{c,i}} \log p(D \mid \beta)... ...{\partial} {\partial \beta_{c,i}} \log p(c_j \mid x_j, \beta)$$ (7)

with a single case $\langle x_j, c_j \rangle$ contributing the following to the gradient of the error for output category $c$ at input dimension $i$:

$$\frac{\partial} {\partial \beta_{c,i}} \log p(c_j \mid x_j, \beta) = x_{j,i} (\textrm{I}(c = c_j) - p(c \mid x_j, \beta))$$ (8)

The derivatives also distribute through the parameters for the Laplace prior:

$$\frac{\partial} {\partial \beta_{c,i}} \log p(\beta_{c,i} \... ..._i} & \textrm{if } \beta_{c,i} < 0 \\ [6pt] \end{array}\right.$$ (9)

Although stochastic gradient is very fast at finding rough solutions, it required tens of thousands of iterations over all of the data to converge within several decimal places.

Training for the large feature systems required on the order of 20 machine hours on a single-threaded single-process estimator. Training of the reduced feature set experiment was quite fast.