Next: MAP Estimates with Laplace Up: Regularized Logistic Regression Previous: Regularized Logistic Regression
A multinomial logistic model classifies ![]() -dimensional real-valued
input vectors
-dimensional real-valued
input vectors
![]() into one of
into one of ![]() outcomes
outcomes
![]() using
using ![]() parameter vectors
parameter vectors
![]() :
:
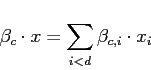 |
(2) |