LENGUAJES REGULARES

	INDICE TEMA 2.- LENGUAJES REGULARES

	1.-Definición Lenguaje Regular
		2.-Autómatas finitos	5.- Tipos de autómatas finitos
		3.-Lenguaje asociado al autómata finito	6.- Operaciones sobre AFND
		4.-Representación de los autómatas finitos	7.- Equivalencia entre autómatas

DEFINICIÓN LENGUAJE REGULAR: Al lenguaje generado por medio de una gramática regular. Son aquellos lenguajes cuyas cadenas está formadas por la concatenación de símbolos, en las cuales no hay relación entre una parte de la cadena y otra parte de la cadena.
Vemos que una gramática regular o de tipo 3 es aquella gramática donde las reglas de producción siguen la siguiente estructura: A→ uB o A→ u donde u∈ T^* y A,B∈ V
OBJETIVO: Encontrar reconocedores para los lenguajes regulares. Estos reconocedores se denominan AUTÓMATAS FINITOS.


AUT�ATAS FINITOS
DEFINICI�: Un aut�ata finito es una quintupla M=(Q,A, d ,q₀,F) en la cual:
Q es un conjunto finito llamado conjunto de estados.
A es un alfabeto llamado alfabeto de entrada.
d es una aplicaci� de la forma siguiente d : Q x A Q de modo que dado un estado y un car�ter del alfabeto se produce otro estado. A esta funci� se le llama funci� de transici�.
q₀es un elemento de Q, llamado estado inicial.
F es un subconjunto de Q, llamado conjunto de estados finales.
El aut�ata es un mecanismo con 2 partes:
Una caja negra de control que va evolucionando por los estados del conjunto Q en funci� del s�bolo le�o de la cinta.

q₀......................................q_n

Una cinta, ilimitada por la derecha, con una cabeza de lectura que inicialmente se sita en la casilla m� a la izquierda.

a	b	...	...	...

FUNCIONAMIENTO: En la cinta se escribe la cadena de caracteres de la que queremos determinar si pertenece al lenguaje regular que poseemos. En cada paso el aut�ata lee un s�bolo y segn el estado en el que se encuentre, cambia de estado y pasa a leer el siguiente s�bolo. As� hasta acabar de leer todos los s�bolos de la cadena, en ese momento si el estado en que est�la flecha o cabeza de lectura es un estado final entonces ACEPTA LA CADENA. Si no es un estado final entonces RECHAZA LA CADENA, es decir, la cadena no pertenece a ese lenguaje regular.

LENGUAJE ASOCIADO A UN AUT�ATA FINITO
El lenguaje que reconoce el aut�ata est�formado por todas aquellas cadenas que se construyen de la siguiente forma: el aut�ata parte de q₀, lee un s�bolo u cualquiera y alcanza un estado final.
Esto se nota de la siguiente forma: L(M)={u�/font> A^* / d (q₀,u)�/font> F}, donde M es el aut�ata finito definido como M=(Q,A, d ,q₀,F) .
Ejemplo 1: Qu�lenguaje reconoce el aut�ata dibujado abajo?

Ejemplo 2 :Qu�lenguaje reconoce el aut�ata dibujado abajo?


REPRESENTACION DE LOS AUT�ATAS FINITOS.-
Existen dos formas de representar los aut�atas:
Se representan mediante un Grafo de Transici� donde:
Los nodos representan estados, habr�tantos nodos como \|Q\| , cada nodo estar� etiquetado por un elemento de Q.
Los arcos representan las transiciones entre los estados. Se etiquetan con el s�bolo que corresponde a esa transici�.
El estado inicial estar�se�lado mediante el s�bolo .
Losestados finales estar� se�lados mediante el simbolo *, o doble c�culo alrededor de la etiqueta del estado final.

EJEMPLO: Realizar el grafo de transici� del aut�ata especificado de la siguiente forma: M=(Q, A, q₀, d , F) donde Q={q₀, q₁, q₂} A={a,b} F={q₂}
	d(q₀,a)=q₁	d(q₀,b)=q₂	d(q₁,a)=q₁	d(q₁,b)=q₂	d(q₂,a)=q₁	d(q₂,b)=q₀


	Con este otro modo de representar los aut�atas solamente se especifica la tabla de las transiciones poniendo en la primera fila el alfabeto de entrada y en la primera columna el conjunto de estados Q, de modo que para cada s�bolo y estado se asocia un estado al cual se va a ir.

d	A	b
q₀	q₁	q₂
q₁	q₁	q₂
q₂	q₁	q₀


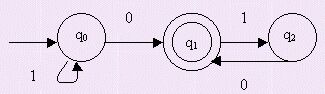
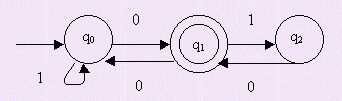
	OPERACIONES SOBRE AUT�ATAS FINITOS NO DETERMIN�TICOS: Si tenemos un lenguaje L1 que es aceptado por un aut�ata finito no determin�tico AFND 1 y otro lenguaje L2 que es aceptado por un aut�ata finito no determin�tico AFND2, entonces podemos: Ejemplo: Construir un AFND con TN que reconozca L1�/font>L2 siendo L1={u10v / u, v�/font> {0,1}} y L2={u00v /u, v�/font> {0,1}} donde sus AFND son los siguientes: AFND 1 Y AFND2
	Ejemplo: Construir un AFND con TN que reconozca la concatenaci� de L1 y L2

	TIPOS DE AUT�ATAS FINITOS.-
	AUT�ATAS FINITOS DETERMIN�TICOS (AFD)
	AUT�ATAS FINITOS NO DETERMIN�TICOS (AFND)
	AUT�ATAS FINITOS NO DETERMIN�TICOS CON TRANSICIONES NULAS (AFND CON TN)
	AUT�ATAS FINITOS NO DETERMIN�TICOS SIN TRANSICIONES NULAS. (AFND SIN TN)

	DEFINICION: AUT�ATAS FINITOS DETERMIN�TICOS (AFD)
	Son aquellos que tienen un nmero finito de estados, q₀, .....,q_n donde n�/font> N. Dentro de estos aut�atas llamaremos AUT�ATA FINITO DETERMIN�TICO MINIMAL a aquel que tiene el menor nmero de estados posibles y sigue reconociendo las cadenas del lenguaje regular.
	EJEMPLO AUT�ATAS FINITOS DETERMIN�TICOS
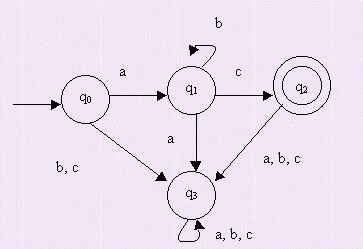
	L={u�/font> {a,b,c}* / u=abⁱc i=0}

	DEFINICION :AUT�ATAS FINITOS NO DETERMIN�TICOS (AFND)
	Son aquellos que tienen un nmero finito de estados, q₀, .....,q_n donde n�/font> N, y es no determin�tico porque no para todo estado y todo s�bolo se tiene una acci� a realizar. Es decir de un nodo no pueden salir varios arcos con la misma etiqueta y ni para un nodo existen arcos para todos los s�bolos del alfabeto
	EJEMPLO: AUT�ATAS FINITOS NO DETERMIN�TICOS
	L={u�/font> {a,b,c}* / u=abⁱc i=0}
	DEFINICI� :AUT�ATAS FINITOS NO DETERMIN�TICOS CON TRANSICIONES NULAS (AFND CON TN)
	Son aquellos que pueden realizar una transici� sin consumir entrada. Estas transiciones se etiquetan con el s�bolo de vac�e en el grafo. En la definici�, habr�que cambiar la funci� de transici� definida como d : Q x A Q de la siguiente forma d : Q x (AU{e }) Q. Las transiciones nulas hacen que el aut�ata pueda quedarse en el estado en el que est� o cambiar de estado sin consumir ningn s�bolo de la palabra de entrada. Sin embargo el conjunto de lenguajes aceptado por este tipo de aut�ata es el mismo que para los AFD.
	EJEMPLO AUT�ATAS FINITOS NO DETERMIN�TICOS CON TRANSICIONES NULAS.
	L={u�/font> {0,1,2}* /u=0ⁱ1^j2^k; i,j,k�/font> N}
	DEFINICI� : AUT�ATAS FINITOS NO DETERMIN�TICOS SIN TRANSICIONES NULAS (AFND SIN TN)
	Se caracteriza porque en � no existen transiciones nulas y puede existir m� de un estado final.
EJEMPLO AUT�ATAS FINITOS NO DETERMIN�TICOS SIN TRANSICIONES NULAS. Un aut�ata finito no determin�tico sin transiciones nulas puede ser el dibujado en el apartado de aut�atas no determin�tico.

	EQUIVALENCIA ENTRE AUT�ATAS
		EQUIVALENCIA ENTRE AFND CON TN Y AFND.
	Sea un AFND con TN especificado por la quintupla M=(Q,A,q₀,d ,F) el AFND equivalente es M`=(Q`, A`, q₀`,d `,F`) donde:
	Q`=ser� el mismo conjunto de estados que se tiene en el AFND con TN, por tanto , Q.
	A`=A.
	q₀`=q0.
	d`(q,u) = conjunto de estados al que se puede pasar leyendo el s�bolo u y aquellos estados a los que se llegue mediante e despu� o viceversa.
	F`= FU{q₀; si puedes llegar de estado q₀ al estado final solamente usando transiciones nulas}
	EJEMPLO: Sea el aut�ata AFND con TN que reconoce el lenguaje L={aⁱb²ⁿc^jd^k / i,j=0,1, n,k�/font> N} especificado por la quintupla:
	M=(Q={q₀,q₁,q₂,q₃}, A={a,b,c,d}, d , q₀, F={q₃})
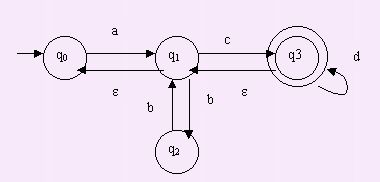	Obtener el AFND.

	EQUIVALENCIA ENTRE AFND Y AFD .
	Sea un AFND especificado por la quintupla M=(Q,A,q₀,d ,F) el AFD equivalente es M`=(Q`, A`, q₀`,d `,F`) donde:
	Q`= conjunto de estados formado por todos los subconjuntos que se puedan formar con los elementos de Q, es decir P(Q).
	A`= el alfabeto del AFND, A.
	q₀`= es el subconjunto de P(Q) que contiene todos los estados iniciales del AFND de partida.
	d`(A,a)= � (x,a) " x�/font> A donde A= subconjunto de estados.
	F`= todos los subconjuntos de estados que contienen al menos 1 estado final del AFND.
	EJEMPLO: dado el AFND que acepta un lenguaje en el que no aparecen 2 b consecutivas especificado por la quintupla:
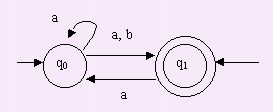
	M=(Q={q₀,q₁}, A={a,b}, {q₀,q₁},d , F={q₁}) Obtener el AFD que acepte ese lenguaje.

EQUIVALENCIA ENTRE AFD Y AFD MINIMAL. ALGORITMO: 1.- Eliminar del AFD los estados innacesibles, es decir, que no se pueden alcanzar, desde el estado inicial. 2.- para cada pareja de estados (q_i, q_l): si uno de los dos estados q_i q_l �/font> F entonces Distinguible(q_i, q_l)=V en una tabla con N estados sin incluir q₀ como filas y como columnas N estados sin incluir el ltimo estado:

3.- Para cada pareja que an no se ha marcado como V (verdad): (q_i, q_j) entonces 3.1- Para cada s�bolo del alfabeto a�/font> A. 3.1.1.- Determino que pareja de estados se puede llegar leyendo a (q_i,q_j) ^a(q_k,q_l) 3.1.2.- Si Distinguible (q_k,q_l)=V y q_kq_l entonces Distinguible(q_i,q_j)=V tambi� marcamos como distinguibles todas las parejas de la lista asociada a q_i, q_jequivalente L(q_i,q_j) 3.1.3.- Si q_k q_l y Distinguible (q_k,q_l)=F entonces L(q_k,q_l)�/font> {(q_i,q_j)} L(q_k,q_l) 3.1.4.- Si q_k= q_l no se hace nada. Estos pasos se repiten hasta que todas las parejas de estados tengan en la tabla V.

	EJEMPLO DE MINIMIZACION
	Dado el AFD Obtener el AFD minimal.

	OTRA FORMA DE MINIMIZAR LOS AUT�ATAS FINITOS DETERMIN�TICOS:
	Esta minimizaci� se realiza teniendo en cuenta la relaci� de equivalencia que induce el AFD.
	DEFINICI� DE RELACI� DE EQUIVALENCIA.-
	Sea L�/font> A* un lenguaje arbitrario. Asociado a este lenguaje L podemos definir una relaci� de equivalencia R_L en el conjunto A* de la siguiente forma:
	Si x, y �/font> A* entonces (xR_L y) si y solo si (" z�/font> A*; x,z�/font> L �/font> yz�/font> L)
	Esta relaci� de equivalencia dividir�el conjunto A* en clases de equivalencia. El nmero de clases de equivalencia se llama �dice de la relaci�.
	ALGORITMO:
	1.- Obtener e identificar las clases que definen todas las cadenas del lenguaje. Y obtener e identificar la clase que est�formada por cadenas que nunca van a pertenecer al lenguaje.
	2.-Las clases de equivalencia definen los estados del aut�ata.
	Estado final �/font> clase de equivalencia que contiene las cadenas de L.
	Estado inicial �/font> clase de equivalencia [e ].
	Las transiciones �/font> Si u, v�/font> A* entonces uR_Lv sii (d `(q₀,u)=d `(q₀,v))
	EJEMPLO: Obtener el AFD minimal que reconoce el siguiente lenguaje L=010

	EJEMPLO 2.- Obtener el AFD minimal que reconoce el siguiente lenguaje L=1⁺01*.