

Cada objeto del TDA Pila modela una pila de elementos de la clase T. Una pila es una clase particular de lista en la que todas las inserciones y borrados tienen lugar en un extremo denominado “cabeza” o “tope”, son listas de tipo LIFO (Last in, First out).
Son objetos mutables, residen en memoria dinámica.
Dentro del TDA Pila hemos propuesto las siguientes primitivas, aunque esto no quiere decir que sean las mejores ni las más adecuadas para todos los casos:
· Pila () -> constructor primitivo, nos crea una pila vacía.
· Pila (const Pila<T> &p) -> constructor de copia, crea una pila que es copia p.
PARÁMETROS : p -> pila que se copia.
· Bool vacia () const -> informa si la pila está vacía, devuelve true si la pila está vacía, false en otro caso.
· T& elemento () -> acceso al elemento en lo alto de la pila, devuelve una referencia al elemento en el tope de la pila.
· Void poner (const T & elem) -> deposita un elemento en la pila, inserta un nuevo elemento en la pila.
PARÁMETROS : elem -> elemento que se inserta.
· Void quitar () -> quita un elemento de la pila, elimina el elemento en lo alto de la pila.
PRECONDICIÓN : el receptor no puede estar vacío.
· ~Pila () -> destructor, el receptor es destruido liberando todos los recursos que usaba.
POSTCONDICIÓN : el receptor es modificado.
En este apartado vamos a mostrar un ejemplo para que comprendamos el funcionamiento de las primitivas del TDA Pila:
Reemplazar un elemento por otro
Este función reemplaza el valor viejo por el nuevo en la pila p, si existe viejo en p.
Pila<int> p;
Void Reemplazar ( int nuevo, int viejo)
{
Pila<int> q = new Pila;
int aux;
while (!p.vacia())
{
aux=p.elemento();
if (aux == viejo)
q.poner(nuevo);
else q.poner(aux);
p.quitar()
}
while (!q.vacia())
{
aux=q.elemento();
q.quitar()
p.poner(aux);
}
}
Cálculo de coeficientes binomiales
Este función nos calcula los coeficientes binomiales, es decir:
![]()
int Comb (int n, int m)
{
Pila<int> pila;
int suma = 0;
pila.poner(n);
pila.poner(m);
while (!pila.vacia())
{
m = pila.elemento();
pila.quitar();
n = pila.elemento();
pila.quitar();
if ((n == 1) || (m == 0) || (m == n))
suma++;
else {
pila.poner(n - 1);
pila.poner(m - 1);
pila.poner(n - 1);
pila.poner(m);
}
}
return suma;
}
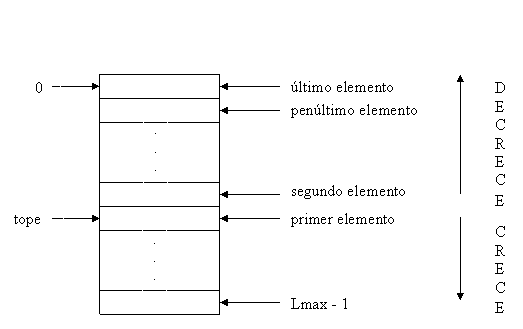
La implementacion basada en vectores o matrices para las listas vistas antes, no es particularmente buena para las pilas, porque cada poner o quitar requiere mover la lista entera hacia arriba o hacia abajo y por tanto, requiere un tiempo proporcional al número de elementos en la pila. Una forma mejor de usar matrices toma en cuenta el hecho de que inserciones y borrados ocurren solamente en el tope y por lo tanto dichas operaciones sólo se efectuarán en un extremo de la estructura. Obsérvese que la mejora puede ser introducida haciendo las nserciones y borrados al final de la lista dentro de la implementación matricial de las listas. Podemos situar el fondo de la pila en el primer elemento de la matriz y hacer crecer la pila hacia el ultimo elemento de la matriz. Un cursor llamado tope indica la posición actual del primer elemento de la pila.
De este modo tenemos un vector elementos donde almacenaremos los elementos que contiene la pila, también tenemos Lmax, el cual nos dice las posiciones que hay reservadas en la pila, y tope que es el elemento de la cabeza de la pila.
 |
Vamos a especificar a continuación la función de abstracción y el invariante de la representación de este tipo de pila:
Función de Abstracción
Dado el objeto del tipo rep r, r = {elementos, Lmax, tope}, el objeto abstracto al que representa es:
Si r.tope == -1, entonces p = <>
En otro caso : p = < r.elementos[r.tope], r.elementos[r.tope-1],..., r.elementos[0] >
Invariante de Representación
0 < r.Lmax.
-1 <= r.tope < r.Lmax.
r.elementos apunta a una dirección con espacio para al menos r.Lmax componentes de tipo T.
De manera que la clase Pila (con implementación mediante vectores) en C++ tendría el siguiente aspecto:
Class Pila
{
Public:
Pila (const int Longmax);
Pila (const Pila<T> &p);
bool vacia () const;
T& elemento ();
void poner (const T& elem);
void quitar ();
~Pila ();
Private:
T *elementos;
int Lmax;
int tope;
}
Pasemos ahora a ver la implementación de cada una de las primitivas enunciadas con anterioridad en C++:
template <class T>
inline Pila<T>::Pila(const int Longmax)
{
elementos = new T [Longmax];
assert(elementos != 0);
Lmax = Longmax;
tope = -1;
}
template <class T>
inline Pila<T>::Pila(const Pila<T> & p)
{
Lmax = p.Lmax;
tope = p.tope;
elementos = new T [LMax];
assert(elementos != 0);
for (int i = 0; i <= tope; i++)
elementos[i] = p.elementos[i];
}
template <class T>
inline bool Pila<T>::vacia() const
{
return tope == -1;
}
template <class T>
inline T& Pila<T>::elemento()
{
return elementos[tope];
}
template <class T>
inline void Pila<T>::poner(const T & elem)
{
if (tope == Lmax -1)
{
cerr << "Error: Pila llena";
exit(-1);
}
tope++;
elementos[tope] = elem;
}
template <class T>
inline void Pila<T>::quitar()
{
if (!vacia())
tope--;
}
La representación mediante nodos enlazados de una pila es facil, porque poner y quitar operan sólamente sobre el nodo de cabecera, de hecho, las cabeceras pueden ser punteros mejor que nodos completos, ya que no hay noción de posición para las pilas y por tanto no necesitamos representar la posición 1 en una forma análoga a otras posiciones tal y como muestra figura.
 |
Obviamente, el
que las funciones sobre pilas sean más especificas que sobre listas implica que
en general se simplificará la implementación (que responde a la estructura de
la figura anterior).
Puesto que esta implementación se basa en una lista la pila es una lista de tipo T con todos sus componentes.
Especificaremos seguidamente la función de abstracción y el invariante de la representación de este tipo de pila:
Función de Abstracción
Dado el objeto del tipo rep r, el objeto abstracto al que representa es:
p = l, con el tope de la pila en la posición l.primero ().
Invariante de Representación
true.
De manera que la clase Pila (con implementación enlazada) en C++ tendría el siguiente aspecto:
Class Pila
{
Public:
Pila ();
Pila (const Pila<T> &p);
bool vacia () const;
T& elemento ();
void poner (const T& elem);
void quitar ();
~Pila ();
Private:
Lista<T> &pila;
}
Pasemos ahora a ver la implementación de cada una de las primitivas enunciadas con anterioridad en C++:
template <class T>
inline Pila<T>::Pila()
{
}
template <class T>
inline Pila<T>::Pila(const Pila<T> & p) : pila(p.pila)
{
}
template <class T>
inline bool Pila<T>::vacia() const
{
return pila.vacia();
}
template <class T>
inline T& Pila<T>::elemento()
{
return pila.elemento(pila.primero());
}
template <class T>
inline void Pila<T>::poner(const T & elem)
{
pila.insertar(pila.primero(), elem);
}
template <class T>
inline void Pila<T>::quitar()
{
pila.borrar(pila.primero());
}
template <class T>
inline Pila<T>::~Pila()
{
}