Introducción

Grafos en general

 

El origen de la palabra grafo es griego y su significado etimológico es "trazar". aparece con gran frecuencia como respuesta a problemas de la vida cotidiana, algunos ejemplos podrían ser los siguientes:un gráfico de una serie de tareas a realizar indicando su secuenciación  (un organigrama), grafos matemáticos que representan las relaciones binarias, una red de carreteras, la red de enlaces ferroviarios o aéreos o la red eléctrica de una ciudad, (ver la figura 1). En cada caso es conveniente representar gráficamente el problema dibujando un grafo como un conjunto de puntos (nodos o vértices) con líneas conectándolos (arcos).

 

 

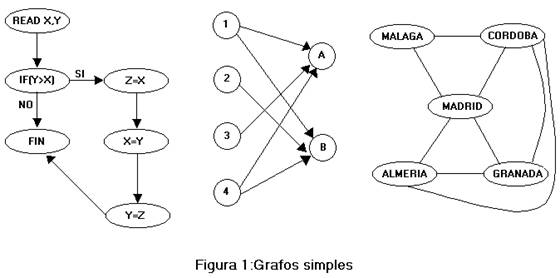
De aquí se podría deducir que un grafo es básicamente un objeto geométrico aunque en realidad sea un objeto combinatorio, es decir,un conjunto de puntos y un conjunto de líneas tomado de entre el conjunto de líneas que une cada par de vértices. Por otro lado, debido a su generalidad y a la gran diversidad de formas que pueden usarse, resulta complejo tratar con todas las ideas relacionadas con un grafo.

 

Para facilitar el estudio de este tipo de dato, a continuación se realizará un estudio de la teoría de grafos desde el punto de vista de las ciencias de la computación, considerando que dicha teoría es compleja y amplia,aquí  sólo se realizará una introducción a la misma, describiéndose el grafo como un tipo de dato y mostrándose los problemas típicos y los algoritmos que permiten solucionarlos usando un ordenador.

 

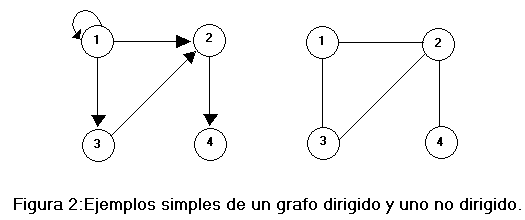
Los grafos son estructuras de datos no lineales que tienen una naturaleza generalmente dinámica, u estudio podría dividirse en dos grandes bloques; grafos dirigidos y grafos no dirigidos (pueden ser considerados un caso particular de los anteriores).

 

Un ejemplo de grafo dirigido lo constituye la red de aguas de una ciudad ya que cada tubería sólo admite que el agua la recorra en un único sentido, por el contrario, la red de carreteras de un país representa en general un grafo no dirigido, puesto que una misma carretera puede ser recorrida en ambos sentidos. No obstante, podemos dar unas definiciones generales para ambos tipos.

 

A continuación daremos definiciones de los dos tipos de grafos y de los conceptos que llevan asociados.

Notación y conceptos

 

Un grafo G es un conjunto en el que hay definida una relación binaria,es decir, G=(V,A) tal que V es un conjunto de objetos a los que denominaremos vértices o nodos y

A Í V x V es una relación binaria a cuyos elementos denominaremos arcos o aristas.

 

Dados x, y Î V, puede ocurrir que:

 

Ø      (x, y)  Î A, en cuyo caso diremos que x e y están unidos mediante un arco y,

 

Ø      (x, y)  Ï A, en cuyo caso diremos que no lo están.

 

Si las aristas tienen asociada una dirección(las aristas (x,y) y (y,x) no son equivalentes) diremos que el grafo es dirigido,en otro caso ((x,y)=(y,x)) diremos que el grafo es no dirigido.

 

 

 

Veamos algunos conceptos sobre grafos:

 

·         Diremos que un grafo es completo si A=VxV,o sea,si para cualquier pareja de vértices existe una arista que los une(en ambos sentidos si el grafo es no dirigido).El número de aristas será:

 

Para grafos dirigidos:        

Para grafos no dirigidos:

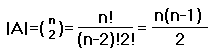
donde n=|V| .

 

·         Un grafo dirigido es simétrico si para toda arista (x, y)  Î A también aparece la arista (y, x)  Î A y es antisimétrico si dada una arista (x, y)  Î A implica que (y, x)  Ï A.

 

·         Tanto a las aristas como a los vértices les puede ser asociada información, a esta información se le llama etiqueta, si la etiqueta que se asocia es un número se le llama peso,costo o longitud, un grafo cuyas aristas o vértices tienen pesos asociados recibe el nombre de grafo etiquetado o ponderado.

 

·         El número de elementos de V se denomina orden del grafo, un grafo nulo es un grafo de orden cero.

 

·         Se dice que un vértice x es incidente a un vértice y si existe un arco que vaya de x a y ((x, y)  Î A),a x se le denomina origen del arco y a y extremo del mismo, de igual forma se dirá que y es adyacente a x, en el caso de que el grafo sea no dirigido si x es adyacente (resp. incidente) a y entonces y también es adyacente (resp. incidente) a x.

 

·         Se dice que dos arcos son adyacentes cuando tienen un vértice común que es a la vez origen de uno y extremo del otro.

 

·         Se denomina camino (algunos autores lo llaman cadena si se trata de un grafo no dirigido)en un grafo dirigido a una sucesión de arcos adyacentes:
C={(v₁,v₂),(v₂,v₃),...,(v_n-1,v_n), v_i Î V}.

 

·         La longitud del camino es el número de arcos que comprende y en el caso en el que el grafo sea ponderado se calculará como la suma de los pesos de las aristas que lo constituyen.

 

·         Un camino se dice simple cuando todos sus arcos son distintos y se dice elemental cuando no utiliza un mismo vértice dos veces.Por tanto todo camino elemental es simple y el recíproco no es cierto.

 

·         Un camino se dice Euleriano si es simple y además contiene a todos los arcos del grafo.

 

·         Un circuito (o ciclo para grafos no dirigidos) es un camino en el que coinciden los vértices inicial y final, un circuito se dice simple cuando todos los arcos que lo forman son distintos y se dice elemental cuando todos los vértices por los que pasa son distintos. La longitud de un circuito es el número de arcos que lo componen. Un bucle es un circuito de longitud 1 (están permitidos los arcos de la forma (i,i) y notemos que un grafo antisimétrico carecería de ellos).

 

·         Un circuito elemental que incluye a todos los vértices de un grafo lo llamaremos circuito Hamiltoniano.

 

·         Un grafo se denomina simple si no tiene bucles y no existe más que un camino para unir dos nodos.

 

·         Diremos que un grafo no dirigido es bipartido si el conjunto de sus vértices puede ser dividido en dos subconjuntos (disjuntos) de tal forma que cualquiera de las aristas que componen el grafo tiene cada uno de sus extremos en un subconjunto distinto, un grafo no dirigido será bipartido si y sólo si no contiene ciclos con un número de aristas par.

 

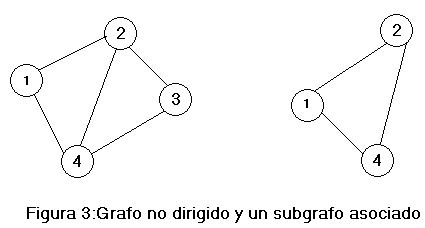
·         Dado un grafo G=(V,A),diremos que G^'=(V,A^' ) con A^' Ì A es un grafo parcial de G y un subgrafo de G es todo grafo G^'=(V^',A^') con V^' Í V y  A^' Í A donde A^' será el conjunto de todas aquellas aristas que unían en el grafo G dos vértices que están en V^'., se podrían combinar ambas definiciones dando lugar a lo que llamaremos subgrafo parcial .

 

 

·         Se denomina grado de entrada de un vértice x al número de arcos incidentes en él, se denota  d_e (x).

 

·         Se denomina grado de salida de un vértice x al número de arcos adyacentes a él, se denota d_s (x).

 

·         Para grafos no dirigidos tanto el grado de entrada como el de salida coinciden y hablamos entonces de grado y lo notamos por d (x).

 

·         A todo grafo no dirigido se puede asociar un grafo denominado dual construido de la siguiente forma:

 

G (V, A) ------> G^' (V^', A^' )

donde A' está construido de la siguiente forma: si e₁,e₂ Î a A son adyacentes --> (e₁,e₂) Î a A' con e₁,e₂ Î a V', en definitiva, para construir un grafo dual se cambian vértices por aristas y viceversa.

 

 

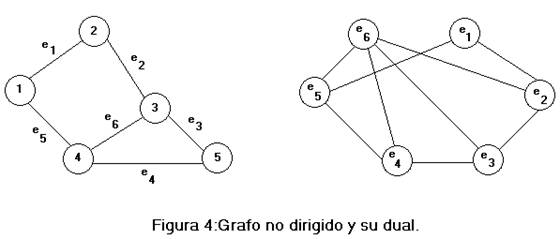
·         Dado un grafo G, diremos que dos vértices están conectados si entre ambos existe un camino que los une.

 

·         Llamaremos componente conexa a un conjunto de vértices de un grafo tal que entre cada par de vértices hay al menos un camino y si se añade algún otro vértice esta condición deja de verificarse. Matemáticamente se puede ver como que la conexión es una relación de equivalencia que descompone a V en clases de equivalencia,cada uno de los subgrafos a los que da lugar cada una de esas clases de equivalencia constituiría una componente conexa. Un grafo diremos que es conexo si sólo existe una componente conexa que coincide con todo el grafo.

Búsqueda de caminos mínimos en grafos

 

Supongamos que tenemos un grafo dirigido sencillo etiquetado G = {V, A} de grado n, V =  {1,..., n} y con etiquetas en los arcos no negativas.

 

Entre un vértice y todos los demás vértices del grafo

 

Nos planteamos el problema de dado un vértice determinar el camino de costo mínimo de ese vértice a todos los demás vértices de V.

 

Para resolver el problema aplicaremos un algoritmo debido a Dijkstra que esencialmente era a partir de un conjunto S de vértices (S Ì V) cuya distancia más corta desde el origen es conocida y en cada paso se agrega un nuevo vértice v a S cuya distancia a su vez desde el origen sea la más corta posible. Si la suposición que hacíamos de que las etiquetas son siempre no negativas se cumple, puede comprobarse que siempre es posible encontrar un camino más corto desde el origen y un vértice v que sólo pase a través de los vértices de S (camino "inherente"). Si se utiliza además un vector D donde se almacena las longitudes de los caminos inherentes más cortos a cada vértice, una vez que S incluya a todos los vértices, todos los caminos son inherentes de forma que D contendrá la distancia más corta del origen a cada vértice.

 

Notación:

 

·        Origen = vértice 1 (obviamente esto no es una condición)

 

·        Sea S un vector de n componentes representando el conjunto de vértices cuya distancia más corta desde el origen ya es conocida.

 

·        D es un vector de n componentes donde D [i] indica en cada paso la distancia más corta entre el origen y el vértice i:

 

a. bien mediante el camino directo si existe el arco (i,j).

 

b. bien a través de los vértices de S (de los que se conoce su distancia más corta al origen),

 

Al final D contendrá el costo del camino mínimo entre el origen y cada vértice.

 

·        C es la matriz de costos del grafo. C [1,i] representa el costo del arco (1,i). Si el arco no existe, se le asigna un valor fuera de rango (¥)

 

·        P es un vector de dimensión n a través del cual reconstruiremos el camino más corto del origen al resto de los vértices. Así P[i] contiene el vértice inmediato anterior a i en el camino más corto.

 

Inicialmente es evidente que S = {1} y  "i  D[i] = C[1 i] con P[i] = 1

Con estas premisas el algoritmo de Dijkstra se puede esquematizar así:

 

Algoritmo Dijkstra()

 

1. S = {1}

 

2. for (i = 2;  i<=n;  i++ )

         {

         D[i] = C[I,i]

         P[i] = 1

         } 

 

3. while ( S ¹ V )

         {

         elegir w Î V-S / D[w] sea mínimo

         S= S U{w}

         for (cada vértice v Î V -S)

               if (D[v] > D[w] + C[w, v])

                  {

                  D[v] = D[w] + C[w, v]

                  P[v] = w

               }

         }

 

            Veamos un ejemplo del algoritmo, supongamos que queremos encontrar los caminos mínimos del vértice 1 al resto en el grafo siguiente:

 

 

           

 

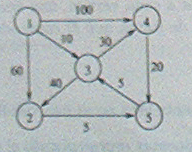
En principio:

 

·        S= {1}

 

·        D [2] = 60; D [3] = 10; D [4] = 100; D [5] = ¥

 

·        P[i] = 1 "i

 

Iteraci6n 1:

 

V -S = {2,3,4,5} w = 3 -> S = {1,3} -> V -S = {2,4,5}

 

D [2] = min(D [2] , D [3] + C [3,2]) = min(60, 50) = 50 -> P [2] = 3

 

D [4] = min(D [4] , D [3] + C [3,4]) = min(100, 40) = 40 -> P [4] = 3

 

D [5] = min(D [5] , D [3] + C [3,5]) = min (¥,¥) = ¥

 

Así D [2] = 50; D [4] = 40; D [5] = 00; P [2] = 3; P [4] = 3; P [5] = 1

 

Iteraci6n 2:

 

V -S = {2,4,5} w = 4 -> S = {1,3,4} -> V- S = {2,5}

 

D [2] = min(D [2] , D [4] + C [4,2]) = min(50, 00) = 50 -> P [2] = 3

 

D [5] = min(D [5] , D [4] + C [4,5]) = min( 00,60) = 60 -> P [5] = 4

 

Así D [2] = 50; D [5] = 60; p [2] = 3; P [5] = 4

 

Iteraci6n 3:

 

V -S = {2,5} w = 2 -> S = {1,3,4,2} -> V- S = {5}

 

D [5] = min(D [5] , D[2] + C [2,5]) = min(60, 55) = 55 -> P [5] = 2

 

Así D [5] = 55; P[5] = 2

 

Finalmente w = 5 -> S = {1,3,4,2,5} -> FIN DEL ALGORlTMO

 

 

Para reconstruir el camino más corto del origen a cada vértice, se asignan los predecesores en orden inverso. Por ejemplo, si se quiere conocer el camino desde el origen al vértice S, se ,tiene que:

 

P [5] = 2-+ P [2] = 3-+ P [3] = 1 siendo por tanto el camino (1,3,2,5) con costo 55 .

 

Aunque la implementación de este algoritmo es simple si la realizamos en base a una matriz de adyacencia, en la práctica se utiliza normalmente una implementación en base a listas de adyacencia. La razón de esta elección es que en la primera la eficiencia es O(n²) para cualquier grafo; sin embargo la mayoría de los grafos que nos encontramos en la práctica tiene un número de aristas bastante pequeño (grafos que podemos denominar dispersos o no densos ) y por tanto el uso de listas de adyacencia se presenta como una solución más eficiente. Para conseguir una mejor eficiencia en esta implementación del algoritmo de Dijkstra se ha echado mano de una estructura de datos formada por un APO que tiene como etiqueta los vértices del grafo y como clave el coste de ir desde el vértice inicial en el problema a ese vértice de tal forma que obtener el vértice con mínimo coste sería O(log n).

Entre cada par de vértices del grafo

 

En lugar de buscar los caminos mínimos de un vértice a los demás nos podemos plantear buscar el camino más corto entre cualquier pareja de vértices, es decir, dado un grafo dirigido etiquetado G = {V, A} en el que las etiquetas son no negativas encontrar el camino de longitud " más corta entre dos vértices cualesquiera de ese grafo.

 

Podría pensarse, para resolver el problema, en aplicar el algoritmo de Dijkstra n veces, una por vértice, pero en lugar de eso, aplicaremos un nuevo algoritmo creado por Floyd que va encontrando los caminos de forma iterativa.

 

Notación:

 

·        V = {1, ..., n} conjunto de vértices.

 

·        A es una matriz de tamaño n x n en la que se calculará en cada A_ij la longitud más corta del camino que va de i a j.

 

·        P es una matriz de tamaño n x n que utilizaremos para recuperar los caminos más cortos.

 

·        C es una matriz de dimensión n x n conteniendo los costos de los arcos. Si no existe arco de un

vértice i a otro j el correspondiente valor C [i,j] = ¥. 

 

Inicialmente A [i,j] = { C[i,j] si i ¹ j, 0 si i = j }.

 

A continuación se itera sobre A n veces de forma que tras hacer la k iteración A[i,j] tiene un valor correspondiente a la longitud más pequeña de cualquier camino de i a j que no pase por un vértice de índice mayor que k, es decir, cualquier vértice intermedio entre i y j (extremos del camino) ha de ser menor o igual que k. Por tanto en cada iteración k se usará la siguiente fórmula:

 

A_k [i,j] = min(A_k-1 [i,j] ,A_k-1 [i,k] +A_k-1l [k,j])³ es decir, cada A_k [i,j] se obtiene comparando A_k-1 [i,j], el coste de ir de i a j sin pasar por k o cualquier vértice de índice mayor, con A_k-1 [i,k] +A_k-1 [k,j], el costo de ir primero de i a k y después de k a j sin pasar por un vértice de índice mayor que k de forma que si el paso por el vértice k produce un camino i más corto que el indicado por A_k-1 [i,j], se elige ese coste para A_k [i,j] .Así mismo, cada iteración P [i,j] contendrá el vértice k que permitió al algoritmo de Floyd encontrar el valor más pequeño de A[i, j] .Inicialmente P[i,j] = 0, puesto que inicialmente el camino más corto de i a j es el propio arco.

 

El algoritmo sería el siguiente:

 

Algoritmo Floyd()

 

1. for (i = 1;  i <= n;  i++ )

          for (j = 1; j <=n ; j++)

               {

               A[i, j]= C[i, j]

               P[i, j]= 0

               }

 

2. for (i = 1; i <= n;  i++)

         A[i, i]= 0

 

3. for (k = 1; k <= n; k++)

          for (i = 1; i <= n; i++)

               for (j = l; j <=n ; j++)

         if ((i ¹ j) && (A[i,k]+A[k,j] < A[i, j]))

            {

            A[i, j]= A[i, k]+A[k, j]

            P[i, j]= k

            }

 

Veamos un ejemplo con el siguiente grafo:

 

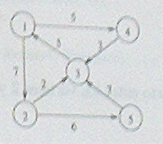
A₀ =                                                                    P₀ =  

0	7	*	5	*
	0	2	*	6
5	*	0	*	*
	*	3	0	*
	*	7	*	0

0	0	0	0	0
0	0	0	0	0
0	0	0	0	0
0	0	0	0	0
0	0	0	0	0

A₁ =                                                                    P₁ =  

0	7	*	5	*
	0	2	*	6
5	[12]	0	10	*
	*	3	0	*
	*	7	*	0

0	0	0	0	0
0	0	0	0	0
0	[1]	0	[1]	0
0	0	0	0	0
0	0	0	0	0

A₂ =                                                                    P₂ =  

0	7	[9]	5	[13]
	0	2	*	6
5	12	0	10	[18]
	*	3	0	*
	*	7	*	0

0	0	[2]	0	2
0	0	0	0	0
0	1	0	1	[2]
0	0	0	0	0
0	0	0	0	0

A₃ =                                                                    P₃ =  

0	7	9	5	13
[7]	0	2	[12]	6
5	12	0	10	18
[8]	[15]	3	0	[21]
[12]	[19]	7	[17]	0

0	0	2	0	2
3	0	0	3	0
0	1	0	1	2
[3]	[3]	0	0	[3]
[3]	[3]	0	[3]	0

A₄ =                                                                    P₄ =  

0	7	[8]	5	13
7	0	2	12	6
5	12	0	10	18
8	15	3	0	21
12	19	7	17	0

0	0	[4]	0	2
3	0	0	3	0
0	1	0	1	2
3	3	0	0	3
3	3	0	3	0

A₅ =                                                                    P₅ =  

0	7	8	5	13
7	0	2	12	6
5	12	0	10	18
8	15	3	0	21
12	19	7	17	0

0	0	4	0	2
3	0	0	3	0
0	1	0	1	2
3	3	0	0	3
3	3	0	3	0

A₅ =A₄  con la que el algoritmo termina. Con objeto de recuperar los caminos de cualquier vértice i a cualquier otro j puede usarse el siguiente procedimiento:

 

Algoritmo recuperar_camino (i, j de tipo vértice)

 

1.k= P[i, j]

 

2. if (k ¹ 0)

       {

       recuperar_camino (i, k)

       escribir (k)

       recuperar_camino (k, j)

       }

 

Por ejemplo, el camino más corto entre los vértices 2 y 4 se determinaría llamando a:

 

recuperar-camino (2,4)

 

k = 3 -> recuperar-camino (2,3) -> 0

[3]

recuperar-camino (3,4) -> k = 1 -> recuperar-camino (3,1) -> 0

[1]

recuperar-camino (1,4) -> 0

 

con la que el camino es (2,3,1,4) con costo 12.

Primitivas del grafo

 

Dentro del TDA Grafo hemos propuesto las siguientes primitivas:

 

·        Grafo ( ) -> constructor del grafo, reserva los recursos e inicializa el grafo a vacío.

 

·        Nodo LocalizaLabel (const Tbase e) -> localiza la etiqueta, devuelve el nodo asociado a la etiqueta e.

PARÁMETROS : e -> etiqueta asociada al nodo a encontrar.

 

·        Bool ExisteArco (nodo o, nodo  d) -> nos dice si existe un arco, devuelve true si existe el arco o false en otro caso.

PARÁMETROS : o -> nodo origen del arco.

       d -> nodo destino del arco.

 

·        Int GrafoVacio () -> devuelve 0 si el grafo esta vacio, si no devuelve 1 en otro caso.

 

·        Float EtiqArco (nodo o, nodo d) -> devuelve la etiqueta asociada a un arco, es decir el peso del arco.

PARÁMETROS : o -> nodo origen del arco.

       d -> nodo destino del arco.

 

·        Void InsertarNodo (const Tbase dato) -> inserta un nodo nuevo en el grafo.

PARÁMETROS : dato -> etiqueta del nuevo nodo.

             

·        Void InsertarArco (nodo o, nodo d, int valor) -> inserta un arco entre el nodo o y el d, asociado al arco le podemos dar un valor o peso.

PARÁMETROS : o -> nodo origen del arco.

       d -> nodo destino del arco.

                   valor ->  peso del del arco.

 

·        Void BorrarArco (nodo o, nodo d) -> borra el arco existente entre los nodos o y d.

PARÁMETROS : o -> nodo origen del arco.

       d -> nodo destino del arco.

 

·        Void DesconectarNodo (nodo a_eliminar) -> elimina un nodo del grafo receptor, todos los arcos que entran o salen del nodo a eliminar tambien desaparecen.

PARÁMETROS : a_eliminar -> nodo a eliminar del grafo.

 

·        Void CopiarGrafo (Grafo gr) -> copia el grafo gr en el receptor.

PARÁMETROS : gr -> grafo a copiar.

 

·        ~Grafo () -> destructor, destruye el grado liberando todos los recursos.

           

 

 

 

Ejemplos de uso

 

Imprimir un grafo

 

Esta función nos imprime en pantalla el contenido de un grafo con etiquetas enteras.

 

Grafo<int> g;

 

Void Imprimir ()

    {

    nodo n1, n2;

    arco a;

    int cont = 1;

 

    printf (“Arcos : \n”);

    for (n1=g.inicio; n1 != 0; n = n->sig)

         {

         if  (n1->etiqueta != 0)

             {

             for (a = n1->ady; a != 0; a = a->sig)

                  {

                  n2 = a->destino;        

                  printf (“%3d -> %3d (%d)”, n1->etiqueta, n2->etiqueta, a->valor);

                  }

             if (cont % 4)

                 printf (“,”);

             else printf (“ \n ”);

             cont++;

             }

         }

    if ((cont % 4) != 0)   

        printf (“ \n ”);

    }

Implementación del Grafo

 

Existen diversas representaciones de naturaleza muy diferente que resultan adecuadas para manejar un grafo,y en la mayoría de los casos no se puede decir que una sea mejor que otra siempre ya que cada una puede resultar más adecuada dependiendo del problema concreto al que se desea aplicar, así,si existe una representación que es peor que otra para todas las operaciones excepto una es posible que aún así nos decantemos por la primera porque precisamente esa operación es la única en la que tenemos especial interés en que se realice de forma eficiente.

 

A continuación veremos dos de las representaciones más usuales:

Matriz de adyacencia

 

Grafos dirigidos

 

G=(V,A) un grafo dirigido con |V|=n .Se define la matriz de adyacencia o booleana asociada a G como B_nxn con :

 

b _i,j = { 1 si (i,j) Î A, 0 en otro caso }

 

Como se puede ver se asocia cada fila y cada columna a un vértice y los elementos b_i,j de la matriz son 1 si existe el arco (i,j) y 0 en caso contrario.

 

Grafos no dirigidos

 

G=(V,A) un grafo no dirigido con |V|=n .Se define la matriz de adyacencia o booleana asociada a G como B_nxn con:

 

b _i,i = { 1 si (i,j) Î A, 0 en otro caso }

 

La matriz B es simetrica con 1 en las posiciones ij y ji si existe la arista (i,j).

 

Veamos ahora un ejemplo:

 

             

 

 

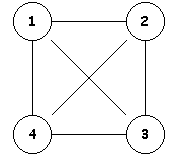
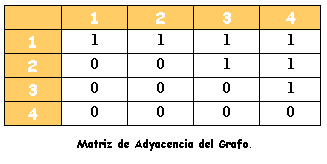
Si el grafo es etiquetado,entonces tanto b_i,j como b_i,j representan al coste o valor asociado al arco (i,j) y se suelen denominar matrices de coste. Si el arco (i,j) no pertenece a A entonces se asigna b_i,j o b_i,j un valor que no puede ser utilizado como una etiqueta valida.

La principal ventaja de la matriz de adyacencia es que el orden de eficiencia de las operaciones de obtencion de etiqueta de un arco o ver si dos vertices estan conectados son independientes del número de vértices y de arcos, por el contrario, existen dos grandes inconvenientes:

 

Ø      Es una representación orientada hacia grafos que no modifica el número de sus vertices ya que una matriz no permite que se le o supriman filas o columnas.

 

Ø      Se puede producir un gran derroche de memoria en grafos poco densos (con gran número de vértices y escaso número de arcos).

 

Para evitar estos inconvenientes se introduce otra representación: las listas de adyacencia.

Lista de adyacencia

 

En esta estructura de datos la idea es asociar a cada vertice i del grafo una lista que contenga todos aquellos vértices j que sean adyacentes a él. De esta forma sóllo reservará memoria para los arcos adyacentes a i y no para todos los posibles arcos que pudieran tener como origen i, el grafo, por tanto, se representa por medio de un vector de n componentes (si |V|=n) donde cada componente va a ser una lista de adyacencia correspondiente a cada uno de los vertices del grafo. Cada elemento de la lista consta de un campo indicando el vértice adyacente. En caso de que el grafo sea etiquetado, habrá que añadir un segundo campo para mostrar el valor de la etiqueta.

 

Veamos un ejemplo a continuación:

 

               

 

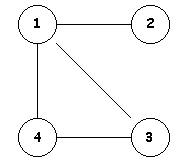
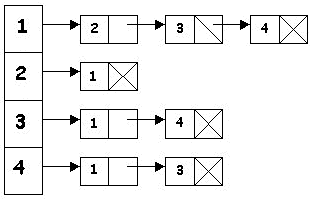
Esta representacion requiere un espacio proporcional a la suma del número de vértices, más el nùmero de arcos, y se suele usar cuando el número de arcos es mucho menor que el número de arcos de un grafo completo. Una desventaja es que puede llevar un tiempo O(n) determinar si existe un arco del vértice i al vértice j, ya que puede haber n vertices en la lista de adyacencia asociada al vértice i.

 

Mediante el uso del vector de listas de adyacencias sólo se reserva memoria para los arcos existentes en el grafo con el consiguiente ahorro de la misma, sin embargo, no permite que haya vértices que puedan ser añadidos o suprimidos del grafo, debido a que la dimension del grafo debe ser predeterminadoa y fija.

 

Para solucionar esto se puede usar una lista de listas de adyacencia, sólo los vértices del grafo que sean origen de algun arco aparecerán en la lista, de esta forma se pueden añadir y suprimir arcos sin desperdicio de memoria ya que simplemente habrá que modificar la lista de listas para reflejar los cambios.

 

         

 

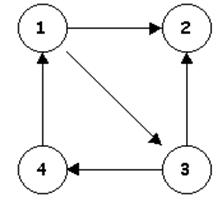
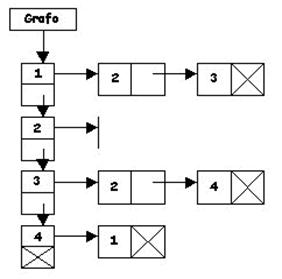
Como puede verse en el ejemplo de las figuras anteriores tanto el vector de listas de adyacencias como en la lista de listas se ha razonado en función de los vértices que actúan como origenes de los arcos. Análogamente se podía haber hecho con lod vertices destino, y combinando ambas representaciones podría pensarse en utilizar dos vectores de listas de adyacencia o dos listas de listas de adyacencia.

 

Nuestra implementacíon es con listas de adyacencia donde sólo usamos los arcos adyacentes y no los incidentes, es una simplificación considerable ya que no tenemos mucho tiempo.

 

Usamos una estructura nodo que simula lo que sería un vértice o nodo del grafo, contine un elemento de tipo Tbase que es la etiqueta, un entero nodo que identifica unívocamente al nodo, un puntero sig al siguiente nodo de la lista y un puntero ady a la lista de adyacencia del nodo en cuestión. Podría tener como hemos comentado antes un puntero a la lista de arcos incidentes pero hemos simplificado el problema.

 

También tenemos otra estructura para simular el comportamiento de un arco o arista del grafo, esta estructura tiene un valor que es el peso que tiene el arco tratado, un puntero sig al siguiente arco de la lista, un puntero al nodo origen del arco y otro al destino del mismo.

 

El grafo se compone de un nodo inicio que es el pirmer nodo del grafo, del cual cuelgan el resto de los nodos y del nnodos que nos da el número de nodos del grafo.

 

Para el grafo de la siguiente figura:

 

 

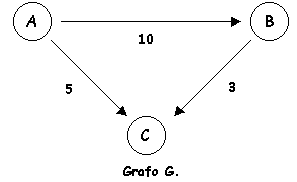
La representación según nuestra implementación sería:

 

 

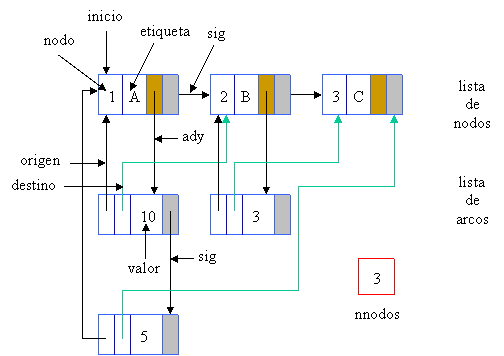Vamos a ver la especificación tanto de la función de abstracción como del invariante de la representación del grafo:

 

Función de Abstracción

 

Dado el objeto del tipo rep r, r = {inicio, nnodos}, el objeto abstracto al que representa es:

 

g = < r.inicio, r.inicio->sig, r.inicio->sig->sig ..., r.inicio->sig... nnodos...->sig >

 

Invariante de Representación

 

0 <= r.nnodos < 5

 

De manera que la clase Grafo en C++ tendría el siguiente aspecto:

 

Class Grafo

       {

       Public:

           struct nodo

              {

              Tbase etiqueta;

                       int nodo;

              struct nodo *sig;

              struct arco *ady;

              }

     

          struct arco

              {

              int valor;

              struct nodo *origen;

                       struct nodo *destino;

              struct arco *sig;

              }

     

          struct nodo *inicio;

          int nnodos;

 

          Grafo ();

          nodo LocalizaLabel (const Tbase e);

          bool ExisteArco (nodo o, nodo  d);

          int GrafoVacio ();

          float EtiqArco (nodo o, nodo d);

          void InsertarNodo (const Tbase dato);

          void InsertarArco (nodo o, nodo d, int valor);

          void BorrarArco (nodo o, nodo d);

          void DesconectarNodo (nodo a_eliminar);

           void CopiarGrafo (Grafo gr);

           ~Grafo();

 

       }

 

Debemos aclarar un par de cosas sobre la implemenetación en C++; sólo tenemos mimbros públicos para facilitar el acceso a los mismos de forma rápido, aunque esta no sea la filosofía más apropiada tratándose de un lenguaje con orientación a objetos, esto se ha hecho así para simplificar en gran medida tanto las primitivas como el código asociado a ellas ya que en la confección de este tutorial no hemos tenido tiempo suficiente para hacer una clase Grafo como dios manda.

 

Si se quiere hacer una clase grafo donde tengamos miembros privados como inicio y nnodos, debemos elaborar primitivas que nos devuelvan cada elemento de una estructura nodo y arco en este caso, serían muchas primitivas pequeñas, luego el resto (las que hemos elegido aquí) habría que modificarlas en base a las nuevas primitivas elaboradas.

 

Pasemos ahora a ver la implementación de cada una de las primitivas enunciadas con anterioridad en C++: