Introducción

Cada objeto del TDA Cola, modela una cola de elementos de la clase T, una cola es un tipo particular de lista en la que los elementos se insertan por un extremo (el final) y se consultan y suprimen por el otro (cabecera). Son listas del tipo FIFO (First In,  First Out).

 

Son objetos mutables, residen en memoria dinámica.

 

 

Primitivas de la cola

 

 

 Dentro del TDA Cola hemos propuesto las siguientes primitivas, aunque esto no quiere decir que sean las mejores ni las más adecuadas para todos los casos:

 

·              Cola () -> constructor primitivo, nos crea una cola vacía.

 

·              Cola (const Cola<T> &c) -> constructor de copia, crea una cola que es copia p.

PARÁMETROS :  c -> cola que se copia.

   

·              Bool vacia () const -> informa si la cola está vacía, devuelve true si la cola está vacía, false en otro caso.

 

·              T& cabecera () -> acceso al elemento al principio de la cola, devuelve una referencia al elemento en la cabecera de la cola.

 

·              Void poner (const T & elem) -> añade un elemento en la cola, inserta un nuevo elemento al final de la cola.

PARÁMETROS :  elem -> elemento que se inserta.

 

·              Void quitar () -> quita un elemento de la cola, elimina el elemento en la cabecera de la cola.

PRECONDICIÓN :  el receptor no puede estar vacío.

 

·              Int num_elementos () -> obtiene el número de elementos incluidos en la cola.

 

·               ~Cola () -> destructor, el receptor es destruido liberando todos los recursos que usaba.

POSTCONDICIÓN :  el receptor es modificado.

Ejemplos de uso

         En este apartado vamos a mostrar un ejemplo para que comprendamos el funcionamiento de las primitivas del TDA Cola:

 

 

Rotar una cola

 

La función rota una cola  un número n  de veces,si está vacía la función no hace nada.

 

Cola<int> c;

 

void rotar (int n)

    {

    int nrotaciones, e;

 

    if  (!c.vacia ())

        {

        nrotaciones = n % c.num_elementos();

        for (int i = 0; i < nrotaciones; i++)

             {            

             e = c.cabecera ();

             c.quitar ();

             c.poner (e);

             }

        }

    }

Implementación de las colas

 

Implementación enlazada

 

Igual que en el caso de las pilas, cualquier implementación de listas es válida para las colas. No obstante, para aumentar la eficiencia de poner es posible aprovechar el hecho de que las inserciones se efectúan sólo en el extremo posterior de forma que en lugar de recorrer la lista de principio a fin cada vez que desea hacer una inserción se puede mantener un apuntador al último elemento, como en las listas de cualquier clase, tambien se mantiene un puntero al frente de la lista, aquí ese puntero es útil para ejecutar mandatos del tipo cabecera o quitar. Utilizaremos al igual que para las listas, un nodo de cabecera con el puntero frontal apuntándola con lo que nos permitirá un manejo más cómodo.

 

Puesto       que esta implementación se basa en una lista la cola es una lista de tipo T con todos sus componentes.

 

 

Veamos la especificación de la función de abstracción y el invariante de la representación de este tipo de cola:

 

 

Función de Abstracción

 

Dado el objeto del tipo rep r, el objeto abstracto al que representa es:

 

c = l, con la cabecera de la cola en la posición l.primero () y el final en la posición l.final ().

 

 

Invariante de Representación

 

true.

 

De manera que la clase Cola (con implementación enlazada) en C++ tendría el siguiente aspecto:

 

Class Cola

       {

       

       Public:

           Cola  ();

           Cola  (const Cola<T>  &c);

           bool vacia () const;

           T& cabecera ();

           void poner (const T& elem);

           void quitar ();

           int num_elementos () const;

           ~Cola ();

 

       Private:

Lista<T> cola;

 

       }

 

 

Pasemos ahora a ver la implementación de cada una de las primitivas enunciadas con anterioridad en C++:

Implementación mediante matrices circulares

 

La implementación matrical de las listas no es muy eficiente para las colas, puesto que si bien con el uso de un apuntador al último elemento es posible ejecutar poner en un tiempo constante, quitar que suprime le primer elemento, requiere que la cola completa ascienda una posición en la matriz con lo que tiene un orden de eficiencia lineal proporcional al tamaño de la cola. Para evitarlo se puede adoptar un criterio diferente, imaginemos a la matriz como un circulo en el que la primera posición sigue a la última, la cola se encuentra en alguna parte de ese círculo ocupando posiciones consecutivas.

 

Tenemos pues un vector elementos con los elementos de la cola, Lmax que denota el número de posiciones que tiene la cola y los punteros post y ant.

 

 

Para insertar un elemento en la cola se mueve el puntero post una posición en el sentido de las agujas del reloj y se escribe el elemento en esa posición, veámoslo en la siguiente figura.

 

 

                        

 

 

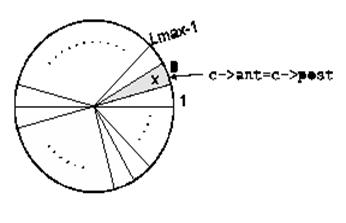
Para suprimir un elemento simplemente se mueve ant una posición en el sentido de las agujas del reloj, de esta forma, la cola se mueve en ese sentido conforme se insertan y suprimen elementos, veámoslo.

 

 

 

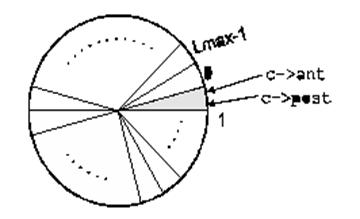
Obsérvese que utilizando este modelo los procedimientos poner y quitar se pueden implementar de manera que su ejecución se realice en tiempo constante.

 

Existe un problema que aparece en la representación  y en cualquier variación menor de esta estrategia (por ejemplo que post apunte a la última posición en el sentido de las agujas del reloj), el problema es que no hay forma de distinguir una cola vacia de una que llene el círculo completo salvo que mantengamos un bit que sea verdad si y solo si la cola está vacia., si no deseamos mantener este bit debemos prevenir que la cola llene alguna vez la matriz.

 

Para ver por qué puede pasar esto, supongamos que la cola de la figura anterior tuviera MAX_LONG elementos, entonces, post apuntaría a la posición anterior en el sentido de las agujas del reloj de ant, ¿qué pasaria si la cola estuviese vacia?, para ver como se representa una cola vacia, consideramos primero una cola de un elemento, entonces post y ant apuntarian a la misma posición, si extraemos un elemento, ant se mueve una posición en el sentido de las agujas del reloj, formando una cola vacia., por tanto una cola vacia tiene post a una posición de ant en el sentido de las agujas del reloj, que es exactamente la misma posición relativa que cuando la cola tenia MAX_LONG elementos, por tanto vemos que aún cuando la matriz tenga MAX_LONG casillas, no podemos hacer crecer la cola más allá de MAX_LONG-1 casillas, a menos que introduzcamos un mecanismo para distinguir si la cola está vacía o llena.

 

                      

 

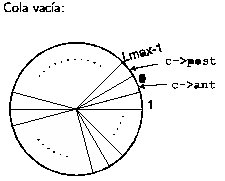
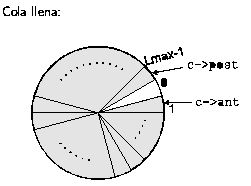
Veamos la especificación de la función de abstracción y el invariante de la representación de este tipo de cola:

 

 

Función de Abstracción

 

Dado el objeto del tipo rep r, r = {elementos, Lmax, ant, post}, el objeto abstracto al que representa es:

 

                     Si r.ant == (r.post + 1) % r.Lmax, entonces c = <>

 

En otro caso :  c = < r.elementos[r.ant], r.elementos[(r.ant+1) % r.Lmax],...,  r.elementos[r.post] >

 

Invariante de Representación

 

0 < r.Lmax.

 

0 <= r.ant < r.Lmax.

 

0 <= r.post < r.Lmax.

 

r.post != r.post.

 

r.elementos apunta a una dirección con espacio para al menos r.Lmax componentes.

 

De manera que la clase Cola (con implementación basada en matrices circulares) en C++ tendría el siguiente aspecto:

 

Class Cola

       {

       

       Public:

           Cola  (int LongMax = 100);

           Cola  (const Cola<T>  &c);

           bool vacia () const;

           T& cabecera ();

           void poner (const T& elem);

           void quitar ();

           int num_elementos () const;

           ~Cola ();

 

       Private:

T *elementos;

const int Lmax;

int ant;

int post;

 

bool llena () const;

       }

 

Pasemos ahora a ver la implementación de cada una de las primitivas enunciadas con anterioridad en C++: