Introducción

Árboles en general

Hasta el momento las estructuras de datos que hemos estudiado eran de tipo lineal, o sea, existía una relación de anterior y siguiente entre los elementos que la componían (cada elemento tendrá uno anterior y otro posterior , salvo los casos de primero y último). Pues bien, aquí se va a estudiar una estructuración de los datos más compleja los árboles, y dentro de estos el árbol binario más concretamente.

Este tipo de estructura es usual incluso fuera del campo de la informática, ejemplos de ello son los árboles gramaticales para analizar oraciones, los árboles genealógicos, representación de jerarquías, etc... La estructuración en árbol de los elementos es fundamental dentro del campo de la informática aplicándose en una amplia variedad de problemas.

En principio podemos considerar la estructura de árbol de manera intuitiva como una estructura jerárquica, por tanto para estructurar un conjunto de elementos e_i en árbol, deberemos escoger uno de ellos e₁ al que llamaremos raíz del árbol, del resto de los elementos se selecciona un subconjunto e₂,...,e_k estableciendo una relación padre-hijo entre la raíz y cada uno de dichos elementos de manera que e₁ es llamado el padre de e₂,de e₃,...e_k y cada uno de ellos es llamado un hijo de e₁. Iterativamente podemos realizar la misma operación para cada uno de estos elementos asignando a cada uno de ellos un número de 0 o más hijos hasta que no tengamos más elementos que insertar. El único elemento que no tiene padre es la raíz del árbol. Por otro lado hay un conjunto de elementos que no tienen hijos aunque sí padre que son llamados hojas. Como hemos visto la relación de paternidad es una relación uno a muchos.

Notación y conceptos

Para tratar esta estructura cambiaremos la nomenclatura, si las listas tenían posiciones, los árboles tienen nodos. Las listas tenían un elemento en cada posición, los árboles tienen una etiqueta en cada nodo. Un árbol sin etiquetas tiene sentido aunque en la inmensa mayoría de los problemas necesitaremos etiquetar los nodos.

 

Usando esta notación, un árbol tiene uno y sólo un nodo raíz y uno o más nodos hoja. Desde un punto de vista formal la estructura de datos árbol es un caso particular de grafo, a los cuales les dedicaremos otro apartado dentro del tutorial, la definición formal más usual de árbol en ciencias de la computación es la recursiva:

 

q       El caso básico es un árbol con un único nodo, lógicamente este nodo es a la vez raíz y hoja del árbol.

 

q       Para construir un nuevo árbol a partir de un nodo n_r y k árboles A₁ ,A₂,...,A_k de raíces n₁,n₂,...,n_k con N₁,N₂,...,N_k elementos cada uno establecemos una relación padre-hijo entre n_r y cada una de las raíces de los k árboles. El árbol resultante de N=1 + N₁ + ... + N_k nodos tiene como raíz el nodo n_r, los nodos n₁,n₂,...,n_k son los hijos de n_r y el conjunto de nodos hoja está formado por la unión de los k conjuntos hojas iniciales. Además a cada uno de los A_i se les denota subárboles de la raíz.

 

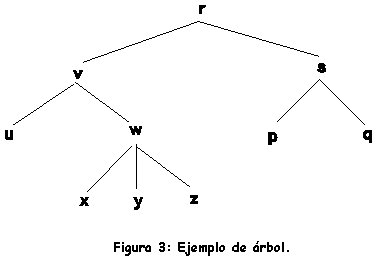
Consideremos el ejemplo de la siguiente figura:

 

 

 

 

Podemos observar que cada uno de los identificadores representa un nodo y la relación padre-hijo se señala con una línea.Los árboles normalmente se presentan en forma descendente y se interpretan de la siguiente forma:

 

q       E es la raíz del árbol.

 

q       S1,S2,S3 son los hijos de E.

 

q       S1,D1 componen un subárbol de la raíz.

 

q       D1,T1,T2,T3,D3,S3 son las hojas del árbol.

 

Además de los términos introducidos consideraremos la siguiente terminología:

 

o        Grado -> número de hijos que tiene, así el grado de un nodo hoja es cero. En la figura anterior el nodo con etiqueta E tiene grado 3.

 

o        Camino -> si n₁,n₂,...,n_k es una sucesión de nodos en un árbol tal que n_i es el padre de n_i+1 para 1 <= i <= k-1 ,entonces esta sucesión se llama un camino del nodo n_i al nodo n_k. La longitud de un camino es el número de nodos menos uno, que haya en el mismo. Existe un camino de longitud cero de cada nodo a sí mismo. Ejemplos sobre la figura anterior: E,S2,D2,T3 es un camino de E a T3 ya que E es padre de S2,éste es padre de D2,etc. S1,E,S2 no es un camino de S1 a S2 ya que S1 no es padre de E.

 

o        Ancestros y descendientes -> si existe un camino, del nodo a al nodo b ,entonces a es un ancestro de b y b es un descendiente de a .En el ejemplo anterior los ancestros de D2 son D2,S2 y E y sus descendientes D2,T1,T2 y T3 (cualquier nodo es a la vez ancestro y descendiente de sí mismo). Un ancestro o descendiente de un nodo distinto de sí mismo, se llama un ancestro propio o descendiente propio respectivamente. Podemos definir en términos de ancestros y descendientes los conceptos de raíz, hoja y subárbol, de este modo en un árbol, la raíz es el único nodo que no tiene ancestros propios, una hoja es un nodo sin descendientes propios y un subárbol de un árbol es un nodo, junto con todos sus descendientes.

 

o        Altura -> la altura de un nodo en un árbol es la longitud del mayor de los caminos del nodo a cada hoja. La altura de un árbol es la altura de la raíz. Ejemplo: en la figura anterior la altura de S2 es 2 y la del árbol es 3.

 

o        Profundidad -> la profundidad de un nodo es la longitud del único camino de la raíz a ese nodo. Ejemplo: en la figura anterior la profundidad de S2 es 1.

 

o        Niveles -> dado un árbol de altura h se definen los niveles 0...h de manera que el nivel i está compuesto por todos los nodos de profundidad i.

 

o        Orden de los nodos -> los hijos de un nodo usualmente están ordenados de izquierda a derecha, si deseamos explícitamente ignorar el orden de los dos hijos, nos referiremos a un árbol como un árbol no ordenado. La ordenación izquierda-derecha de hermanos puede ser extendida para comparar cualesquiera dos nodos que no están relacionados por la relación ancestro-descendiente. La regla a usar es que si n₁ y n₂ son hermanos y n₁ está a la izquierda de n₂, entonces todos los descendientes de n₁ están a la izquierda de todos los descendientes de n₂.

 

Recorridos de un árbol

 

En una estructura lineal resulta trivial establecer un criterio de movimiento por la misma para acceder a los elementos, pero en un árbol esa tarea no resulta tan simple. No obstante, existen distintos métodos útiles en que podemos sistemáticamente recorrer todos los nodos de un árbol. Los tres recorridos más importantes se denominan preorden, inorden y postorden aunque hay otros recorridos como es el recorrido por niveles.

 

Si consideramos el esquema general de un árbol tal como muestra la figura 2 siguiente, los recorridos se definen como sigue:

 

 

El listado en preorden es:

 

q       Si el árbol tiene un único elemento, dicho elemento es el listado en preorden.

 

q       Si el árbol tiene más de un elemento, es decir, una estructura como muestra la figura 2,el listado en preorden es listar el nodo raíz seguido del listado en preorden de cada uno de los subárboles hijos de izquierda a derecha.

 

El listado en inorden es:

 

q       Si el árbol tiene un único elemento, dicho elemento es el listado en inorden.

 

q       Si el árbol tiene una estructura como muestra la figura 2,el listado en inorden es listar el subárbol A₁ en inorden, y listar el nodo raíz seguido del listado en inorden de cada uno de los subárboles hijos de izquierda a derecha restantes.

 

El listado en postorden es:

 

q       Si el árbol tiene un único elemento, dicho elemento es el listado en postorden.

 

q       Si el árbol tiene una estructura como muestra la figura 2,el listado en postorden es listar en postorden cada uno de los subárboles hijos de izquierda a derecha seguidos por el nodo raíz.

 

El listado por niveles sería:

 

Desde i=0 hasta la altura h del árbol, listar de izquierda a derecha los elementos de profundidad i, como podemos observar, un nodo n₁ aparece antes que n₂ en el listado por niveles si la profundidad de n₁ es menor que la profundidad de n₂ usando el orden de los nodos definido anteriormente para el caso en que tengan la misma profundidad.

 

Como ejemplo de listados veamos el resultado que se obtendría sobre el árbol A de la figura.

 

Los resultados de los listados de preorden, postorden e inorden son los siguientes:

 

 -Listado preorden: A=A_r=rA_vA_s=rvA_uA_wA_s=rvuA_wA_s=rvuwA_xA_yA_zA_s=rvuwxA_yA_zA_s =  rvuwxyA_zA_s=rvuwxyzA_s      =rvuwxyzsA_pA_q=rvuwxyzspA_q=rvuwxyzspq.

 

 -Listado postorden :A=A_r=A_vA_sr=A_uA_wvA_sr= uA_wvA_sr=uA_xA_yA_zwvA_sr= uxA_yA_zwvA_sr = uxyA_zwvA_sr=uxyzwvA_sr= uxyzwvA_pA_qsr=uxyzwvpA_qsr=uxyzwvpqsr.

 

-Listado inorden : A=A_r=A_vrA_s=A_uvA_wrA_s= uvA_wrA_s=uvA_xwA_yA_zrA_s=uvxwA_yA_zrA_s=

 uvxwyA_zrA_s=uvxwyzrA_s= uvxwyzrA_psA_q=uvxwyzrpsA_q=uvxwyzrpsq.

 

 

 

Por último, el listado por niveles de este árbol es el siguiente:r,v,s,u,w,p,q,x,y,z.

 

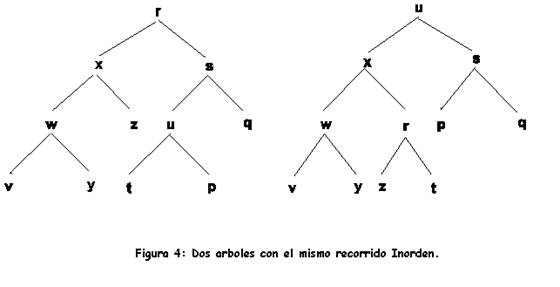
Finalmente es interesante conocer que un árbol no puede, en general,recuperarse con uno solo de sus recorridos. Por ejemplo : dada la lista en inorden vwyxzrtupsq, los árboles de la figura 4 tienen ese mismo recorrido en inorden.

 

Árbol Binario

Un árbol binario puede definirse como un árbol que en cada nodo puede tener como mucho grado 2,es decir,a lo más 2 hijos.Los hijos suelen denominarse hijo a la izquierda e hijo a la derecha,estableciéndose de esta forma un orden en el posicionamiento de los mismos.

Todas las definiciones básicas que se dieron para árboles generales permanecen inalteradas sin más que hacer las particularizaciones correspondientes.

 

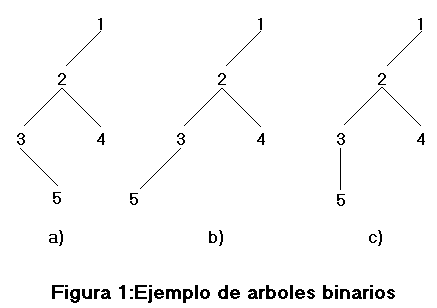
En los árboles binarios hay que tener en cuenta el orden izqda-drcha de los hijos. Por ejemplo:los árboles binarios a) y b) de la figura 1 (adoptamos el convenio de que los hijos a la izquierda son extraídos extendiéndonos hacia la izquierda y los hijos a la derecha a la derecha) son diferentes, puesto que difieren en el nodo 5, el árbol c) por convenio se supone igual al b) y no al a).

 

 

Una instancia del tipo de dato abstracto Árbol Binario sobre un dominio Tbase se puede construir como:

 

·         Un objeto vacío (árbol vacío) si no contiene ningún elemento. Lo denotamos {}.

 

·         Un árbol que contiene un elemento destacado, el nodo raíz, con un valor e en el dominio Tbase (denominado etiqueta), y dos subárboles (T_i izquierdo y T_d derecho) del TDA Árbol Binario sobre Tbase. Se establece una relación padre-hijo entre cada nodo y los nodos raíz de los subárboles (si los hubiera) que cuelgan de él. Lo denotamos {e, {T_i}, {T_d}}

  

El espacio requerido para el almacenamiento es O(n). Donde n es el número de nodos del árbol.

Primitivas del árbol binario

 

Dentro del TDA Árbol Binario hemos propuesto las siguientes primitivas :

 

·        ArbolBinario ( ) -> constructor por defecto, reserva los recursos e inicializa el árbol a vacío.

 

·        ArbolBinario (const Tbase& e) -> constructor de raíz, reserva los recursos e inicializa el árbol con  un único nodo raíz que tiene la etiqueta e.

 

·        ArbolBinario (const ArbolBinario<Tbase>& v) -> constructor de copia, construye el árbol duplicando el contenido de v en el árbol receptor.

PARÁMETROS : v -> ArbolBinario a copiar.

 

·        Void destruir (nodo *n) ->destruye el subárbol, libera los recursos que ocupa n y sus descendientes.

PARÁMETROS : n -> nodo que destruir junto con sus descendientes

             

·        Void copiar (nodo *&dest, nodo  orig) -> copia un subárbol, hace una copia de todo el  subárbol que cuelga de orig en el puntero dest. Es importante ver que en dest->padre (si existe) no se asigna ningún valor, pues no se conoce.

PARÁMETROS : dest -> referencia al puntero del que cuelga la copia.

                                  orig -> puntero a la raíz del subárbol a copiar.

 

·        Void contar (nodo *n) -> cuenta el número de nodos, copia cuántos nodos cuelgan de n, incluído éste.

PARÁMETROS : n -> nodo del que cuelga el subárbol de nodos a contabilizar.

             

·        Bool soniguales (nodo *n1, nodo *n2) -> comprueba igualdad de subárbol, comprueba si son iguales los subárboles que cuelgan de n1 y n2. Para ello deberán tener los mismos nodos en las mismas posiciones y con las mismas etiquetas.

PARÁMETROS : n1 -> primer subárbol a comparar.

                                  n2 -> segundo subárbol a comparar.

 

·        Void escribe_arbol (ostream& out, nodo *nod) const -> escribe un subárbol, escribe en la salida todos los nodos del subárbol que cuelga del nodo nod siguiendo un recorrido en preorden. La forma de impresión de cada nodo es:

                       

- Si el nodo es nodo_nulo, imprime el carácter 'x'

        

- Si el nodo no es nodo_nulo, imprime el carácter 'n' seguido de un espacio, al    que sigue la impresión de la etiqueta.

 

PARÁMETROS : out -> stream de salida donde escribir.

                   nod -> nodo del que cuelga el subárbol a escribir.

 

 

 

 

·        Void lee_arbol (istream& in, nodo *&nod) -> lee un subárbol, lee de la entrada in los elementos de un árbol según el formato que se presenta en la función de escritura.

PARÁMETROS : in -> stream de entrada desde el que leer.

        nod -> referencia al nodo que contendrá el subárbol leído.

 

·        ArbolBinario<Tbase>& operator= (const ArbolBinario<Tbase> &v) ->asignación, asigna el valor del árbol duplicando el contenido de v en el árbol receptor. Devuelve la referencia al árbol receptor.

PARÁMETROS : v -> ArbolBinario a copiar.

 

·        Void asignaRaiz (const Tbase& e) -> asignar nodo raíz, vacía el árbol receptor y le asigna como valor el árbol de un único nodo cuya etiqueta es e.

PARÁMETROS : e -> etiqueta a asignar al nodo raíz.

 

·        Nodo raiz () const -> raíz del árbol, devuelve el nodo raíz, que coincide con nodo_nulo si el árbol está vacío.

           

·        Nodo izquierda (const Nodo n) const -> hijo izquierda, devuelve el nodo hijo a la izquierda de n, que valdrá nodo_nulo si no tiene hijo a la izquierda.

PARÁMETROS : n -> nodo del que se quiere obtener el hijo izquierda, n no es nodo_nulo.

 

·        Nodo derecha (const Nodo n) const -> hijo derecha, devuelve el nodo hijo a la derecha de n, que valdrá nodo_nulo si no tiene hijo a la derecha.

PARÁMETROS : n -> nodo del que se quiere obtener el hijo derecha, n no es nodo_nulo.

 

·        Nodo padre (const Nodo n) const -> nodo padre, devuelve el nodo padre de n, que valdrá nodo_nulo si es la raíz.

PARÁMETROS : n -> nodo del que se quiere obtener el padre, n no es nodo_nulo.

 

·        Tbase& etiqueta (const Nodo n) -> etiqueta en un nodo, devuelve una referencia al elemento del nodo n y por tanto se puede modificar o usar el valor.

PARÁMETROS : n -> nodo en el que se encuentra el elemento,  n no es nodo_nulo.

 

·        Const Tbase& etiqueta (const Nodo n) const -> etiqueta en un nodo, devuelve una referencia al elemento del nodo n , es constante y por tanto no se puede modificar o usar el valor.

PARÁMETROS : n -> nodo en el que se encuentra el elemento,  n no es nodo_nulo.

 

·        Void asignar_subárbol (const ArbolBinario<Tbase>& orig, const Nodo nod) -> copia subárbol, el árbol receptor acaba con un valor copia del subárbol que cuelga del nodo nod en el árbol orig.

PARÁMETROS : orig -> árbol desde el que se va a copiar una rama.

nod -> nodo raíz del subárbol que se copia, es un nodo del árbol orig} y no      es nodo_nulo.

 

·        Void podar_izquierda (Nodo n, ArbolBinario<Tbase>& dest) -> podar subárbol izquierda, asigna un nuevo valor al árbol dest, con todos los elementos del subárbol izquierdo del nodo n en el árbol receptor, este se queda sin dichos nodos.

PARÁMETROS : n -> nodo al que se le podará la rama hijo izquierda, no es nodo_nulo y es    un nodo válido del árbol receptor.

                                  dest -> árbol que recibe la rama cortada.

 

·        Void podar_derecha (Nodo n, ArbolBinario<Tbase>& dest) -> podar subárbol derecha, asigna un nuevo valor al árbol dest, con todos los elementos del subárbol derecho del nodo n en el árbol receptor, este se queda sin dichos nodos.

PARÁMETROS : n -> nodo al que se le podará la rama hijo derecha, no es nodo_nulo y es    un nodo válido del árbol receptor.

                                   dest -> árbol que recibe la rama cortada.

 

·        Void insertar_izquierda (Nodo n, ArbolBinario<Tbase>& rama) -> insertar subárbol, izquierda, el árbol rama se inserta como hijo izquierda del nodo n del árbol receptor. El árbol rama queda vacío y los nodos que estaban en el subárbol izquierdo de n  se eliminan.

PARÁMETROS : n -> nodo al que se insertará el árbol rama como hijo izquierdo. No es  nodo_nulo y es un nodo válido del árbol receptor.

                     rama -> árbol que se insertará como hijo izquierdo.

 

·        Void insertar_derecha (Nodo n, ArbolBinario<Tbase>& rama) -> insertar subárbol, derecha, el árbol rama se inserta como hijo derecha del nodo n del árbol receptor. El árbol rama queda vacío y los nodos que estaban en el subárbol derecho de n  se eliminan.

PARÁMETROS : n -> nodo al que se insertará el árbol rama como hijo derecho. No es  nodo_nulo y es un nodo válido del árbol receptor.

                      rama -> árbol que se insertará como hijo derecho.

 

·        Void clear () -> borra todos los elementos, borra todos los elementos del árbol receptor., cuando termina, el árbol está vacío.

 

·        Int size () const -> número de elementos, devuelve el número de elementos del árbol receptor.

             

·        Bool empty () const -> vacío, devuelve true si el número de elementos del árbol  receptor es cero, false en otro caso.

             

·        Bool operator == (const ArbolBinario<Tbase>& v) const -> igualdad, devuelve true si el  árbol receptor tiene los mismos elementos  y en el mismo orden, false en caso contrario.

PARÁMETROS : v -> ArbolBinario con el que se desea comparar.

             

·        Bool operator != (const ArbolBinario<Tbase>& v) const -> distintos, devuelve true si el árbol receptor no tiene los mismos elementos y en el mismo orden, false en caso contrario.

PARÁMETROS : v -> ArbolBinario con el que se desea comparar.

             

·        Template <class T> friend istream& operator >> (istream& in, ArbolBinario<T>& v)   entrada, lee de in un árbol y lo almacena en v, el formato aceptado para la lectura se puede consultar en la función de salida.

PARÁMETROS : in -> stream de entrada.

                                  v -> árbol que leer.

 

·        Template<class T>friend ostream& operator << (ostream& out, ArbolBinario<T>& v)   salida, escribe en la salida todos los nodos del árbol v siguiendo un recorrido en preorden. La forma de impresión de cada nodo es:

 

- Si el nodo es nodo_nulo, imprime el carácter 'x'

        

- Si el nodo no es nodo_nulo, imprime el carácter 'n' seguido de un espacio, al    que sigue la impresión de la etiqueta.

 

  PARÁMETROS : out -> stream de salida.

                               v -> árbol que escribir.

 

·        ~ArbolBinario () -> destructor, libera los recursos ocupados por el árbol receptor.

Ejemplos de uso

 

Escribir el recorrido en preorden de un árbol binario

 

Esta función escribe en la salida estándar el preorden del subárbol que cuelga del nodo del árbol a.

 

void preorden (const ArbolBinario<int>& a, const  ArbolBinario<int>::Nodo n)

    {

    if (n != ArbolBinario<int>::nodo_nulo)

       {  

       cout << a.etiqueta(n) << ' ';

       preorden(a,a.izquierda(n)); 

       preorden(a,a.derecha(n));     

       }

    }

 

Escribir el recorrido en inorden de un árbol binario

 

Esta función escribe en la salida estándar el inorden del subárbol que cuelga del nodo del árbol a.

 

void inorden(const ArbolBinario<int>& a, const ArbolBinario<int>::Nodo n)

    {

    if (n != ArbolBinario<int>::nodo_nulo)

       {

       inorden(a,a.izquierda(n));

       cout << a.etiqueta(n) << ' ';

       inorden(a,a.derecha(n));

       }

    }

 

Escribir el recorrido en postorden de un árbol binario

 

Esta función escribe en la salida estándar el postorden del subárbol que cuelga del nodo del árbol a.

 

void postorden (const ArbolBinario<int>& a, const ArbolBinario<int>::Nodo n)

    {

    if (n!=ArbolBinario<int>::nodo_nulo)

       {

       postorden(a,a.izquierda(n));        

       postorden(a,a.derecha(n));

       cout << a.etiqueta(n) << ' ';

       }

    }

 

 

Esquema de un árbol binario en ASCII

 

Esta función implementa el esquema de un árbol binario en ASCII. Un ejemplo sería:

El árbol: n 1 n 2 n 4 x x n 5 x n 8 x x n 3 n 6 x x n 7 x x  tiene el esquema:

 

           -- 1

              |-- 3

              |   |-- 7

              |    -- 6

               -- 2

                  |-- 5

                  |   |-- 8

                  |    -- x

 

                   -- 4  

void Esquema (const ArbolBinario<int>& a, const ArbolBinario<int>::Nodo n,  string& pre)

    {

    int i;

    if (n == ArbolBinario<int>::nodo_nulo)

        cout << pre << "-- x" << endl;

    else {

            cout << pre << "-- " << a.etiqueta(n) << endl;

            if (a.derecha(n) != ArbolBinario<int>::nodo_nulo || 

  a.izquierda(n) != ArbolBinario<int>::nodo_nulo)

               {

               pre +="   |";

               Esquema (a,a.derecha(n),pre);

               pre.replace(pre.size()-4,4,"    ");

               Esquema (a,a.izquierda(n),pre);

               pre.erase(pre.size()-4,4);   

               }

           }

    }

 

Reflejo de un árbol binario

 

Esta función implementa la transformación de un árbol binario mediante reflexión. El árbol resultante es un reflejo del original (como si se reflejara en   un espejo).

 

void refleja (ArbolBinario<int>& a)

    {

    ArbolBinario<int> ai,ad;

     

             if (!a.empty())

        {

        a.podar_izquierda(a.raiz(),ai);

        a.podar_derecha(a.raiz(),ad);

        refleja(ai);

        refleja(ad);

        a.insertar_izquierda(a.raiz(),ad);

        a.insertar_derecha(a.raiz(),ai);

        }

    }

Implementación del árbol binario

 

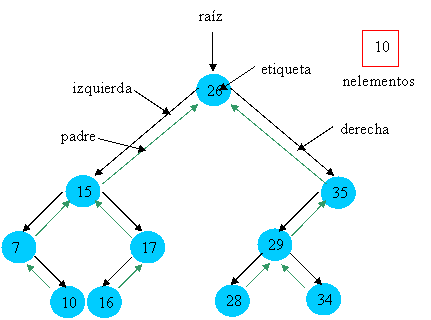
Un árbol binario se compone de un nodo raíz que es un puntero al primer nodo del árbol, vale 0 si el árbol es vacío, nodo es una estructura donde almacenamos una etiqueta del árbol que se implementa como un conjunto de nodos enlazados según la relación padre-hijo, los componentes de la estructura nodo los vamos a describir seguidamente:

 

q       Etiqueta -> es el elemento almacenado en un nodo del árbol, es de tipo Tbase, int, char, etc.

 

q       Izqda -> en este campo de almacena un puntero al nodo raíz del subárbol izquierdo o el valor 0 si no tiene.

 

q       Drcha -> en este campo de almacena un puntero al nodo raíz del subárbol derecho o el valor 0 si no tiene.

 

q       Padre -> en este campo de almacena un puntero al nodo padre o el valor 0 si es la raíz del árbol.

 

Debemos también significar que un nodo nulo es un nodo que apunta a null, o sea, a ningún sitio, no tiene nada y se denota en esta implementación con el número cero.

 

 A continuación veamos un ejemplo de árbol binario:

 

 

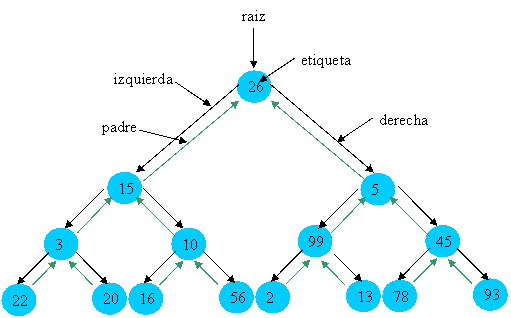Vamos a ver la especificación tanto de la función de abstracción como del invariante de la representación del árbol binario:

 

Función de Abstracción

 

Sea T un árbol binario sobre el tipo Tbase, entonces si lo denotamos también Arbol (T.laraiz), es decir, como el árbol que cuelga de su raíz, entonces éste árbol del conjunto de valores en la representación se aplica al árbol:

 

{ T.laraiz -> etiqueta, {Arbol (T.laraiz -> izqda)}, {Arbol (T.laraiz -> drcha)}}

 

Donde { 0 } es el árbol vacío.

           

Invariante de Representación

 

Sea T, un árbol binario sobre el tipo Tbase, entonces el invariante de la representación es :

               

Si T es vacío, entonces T.laraiz = 0, y si no:

 

T.laraiz -> padre =  0 y

 

"n nodo de T, n -> izqda ¹ n -> drcha y

 

"n, m nodos de T, si n -> izqda = m o n -> drcha = m entonces m ->padre = n.

           

De manera que la clase ArbolBinario en C++ tendría el siguiente aspecto:

 

Class ArbolBinario

       {

       

       Public:

            typedef struct nodo *Nodo;

            static const Nodo nodo_nulo = 0;

           

            ArbolBinario();

            ArbolBinario(const Tbase& e);

            ArbolBinario (const ArbolBinario<Tbase>& v);

            ArbolBinario<Tbase>& operator=(const ArbolBinario<Tbase> &v);

            void AsignaRaiz(const Tbase& e);

            Nodo raiz() const;

            Nodo izquierda(const Nodo n) const;

            Nodo derecha(const Nodo n) const;

            Nodo padre(const Nodo n) const;

            Tbase& etiqueta(const Nodo n);

            const Tbase& etiqueta(const Nodo n) const;

            void asignar_subarbol(const ArbolBinario<Tbase>& orig, const Nodo nod);

            void podar_izquierda(Nodo n, ArbolBinario<Tbase>& dest);

            void podar_derecha(Nodo n, ArbolBinario<Tbase>& dest);

            void insertar_izquierda(Nodo n, ArbolBinario<Tbase>& rama);

            void insertar_derecha(Nodo n, ArbolBinario<Tbase>& rama);

            void clear();

            int size() const;

            bool empty() const;

            bool operator == (const ArbolBinario<Tbase>& v) const;

            bool operator != (const ArbolBinario<Tbase>& v) const;

            template<class T>

            friend istream& operator >> (istream& in, ArbolBinario<T>& v);

            template<class T>

            friend ostream& operator <<  (ostream& out, const ArbolBinario<T>& v);

            ~ArbolBinario();

 

     Private:

 

          struct nodo

              {

              Tbase etiqueta;

              struct nodo *izqda;

              struct nodo *drcha;

              struct nodo *padre;

              };

         

          struct nodo *laraiz;

 

          void destruir(nodo * n);

          void copiar(nodo *& dest, nodo * orig);

          void contar(nodo * n);

          bool soniguales(nodo * n1, nodo * n2);

          void escribe_arbol(ostream& out, nodo * nod) const;

          void lee_arbol(istream& in, nodo *& nod);

 

       }

 

Pasemos ahora a ver la implementación de cada una de las primitivas enunciadas con anterioridad en C++: