Una instancia del tipo de dato abstracto APO sobre un dominio Tbase es un árbol binario con etiquetas en Tbase y un orden parcial que consiste en que la etiqueta de un nodo es menor o igual que la de sus descendientes. Para poder gestionarlo, debe existir la operación menor (<) para el tipo Tbase.
El espacio requerido para el almacenamiento es O(n), donde n es el número de elementos del árbol.
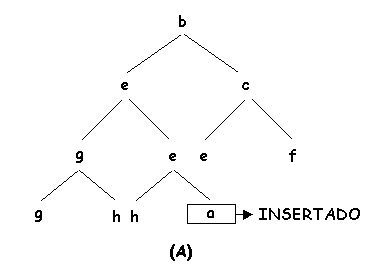
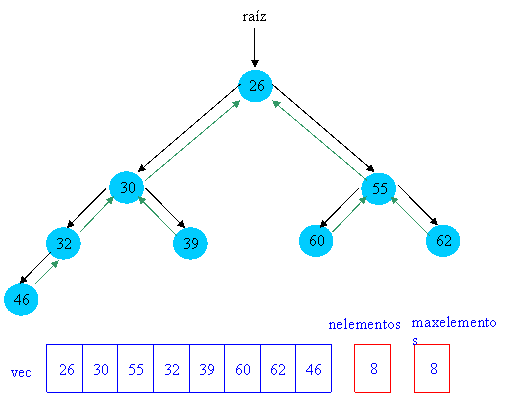
Las operaciones básicas en este tipo de árboles son la de inserción de un elemento y la de borrado del elemento de menor etiqueta (la raíz) ,con la consiguiente problemática que se plantea al tener que dejar el árbol tras cualquier operación tanto equilibrado como cumpliendo la condición de orden parcial. Un ejemplo de este tipo de árboles muestra en la siguiente figura:
Dentro del TDA APO hemos propuesto las siguientes primitivas :
· Apo ( ) -> constructor por defecto, reserva los recursos e inicializa el árbol a vacío.
· Apo (int tam ) -> constructor con tamaño, reserva los recursos e inicializa el árbol a vacío.
PARÁMETROS : tam -> número de elementos que se espera pueda llegar a tener el árbol.
· Apo (const Apo<Tbase>& a) -> constructor de copia, construye el árbol duplicando el contenido de a en el árbol receptor.
PARÁMETROS : a -> Apo a copiar.
· Void expandir (int nelem) -> aumenta la capacidad de almacenamiento, asigna un bloque de memoria para nelem elementos para almacenar la matriz vec, al terminar, vec apunta a un bloque con esa capacidad, conservando el contenido anterior y el miembro maxelementos vale nelem, sim embargo, si nelem es menor o igual que maxelementos no hace nada.
PARÁMETROS : nelem -> nuevo número de casillas reservadas para la matriz vec, nelementos <= nelem.
· Apo<Tbase>& operator = (const ABB<Tbase> &v) ->asignación, asigna el valor del árbol duplicando el contenido de v en el árbol receptor. Devuelve la referencia al árbol receptor.
PARÁMETROS : v -> Apo a copiar.
· Const Tbase& minimo () const -> mínimo elemento almacenado, devuelve una referencia al elemento más pequeño de los almacenados en el árbol receptor.
PRECONDICIÓN : el árbol no está vacío.
· Void borrar_minimo () -> elimina el mínimo, elimina del árbol receptor el elemento más pequeño.
PRECONDICIÓN : el árbol no está vacío.
· Void insertar (const Tbase& el) -> insertar un elemento, inserta el elemento el en el árbol receptor.
PARÁMETROS : param -> nuevo elemento a insertar.
· Void clear () -> borra todos los elementos, borra todos los elementos del árbol receptor., cuando termina, el árbol está vacío.
· Int size () const -> número de elementos, devuelve el número de elementos del árbol receptor.
· Bool empty () const -> vacío, devuelve true si el número de elementos del árbol receptor es cero, false en otro caso.
· ~Apo () -> destructor, libera los recursos ocupados por el árbol receptor.
Ordenar los elementos de un APO
Este programa inserta un conjunto de enteros alaeatorios en el Apo., después los lista todos ordenados borrando en cada iteración uno, es el método heapsort.
#include <cstdlib>
#include <ctime>
#include <iostream>
#include <APO.h>
int main()
{
Apo<int> a(100000);
int i;
srand(time(NULL));
for (i=0;i<100000;i+=2)
a.insertar((int)(1000.0*rand()/RAND_MAX));
while (!a.empty())
{
cout << a.minimo() << ' ';
a.borrar_minimo();
}
cout << endl;
return 0;
}
Un APO es un árbol pero en este caso no se implementa como un árbol binario o un ABB con esas estructuras complejas como nodo. Tenemos un vector de tipo Tbase llamada vec donde alamacenaremos los elementos del APO. Tenemos nelementos que nos da el número de elementos del APO. Por último tenemos maxelementos que nos indica la cantidad de posiciones reservadas en vec, como es natural debe ser mayor o igual a nelementos.
 |
Vamos a ver la especificación tanto de la función de abstracción como del invariante de la representación del APO:
Función de Abstracción
Sea T un árbol parcialmente ordenado sobre el tipo Tbase, diremos que el subárbol a partir de la posición i es:
- Si 0 <= i < nelementos el que tiene como elemento raíz el valor T.vec[i] y como subárboles izquierda y derecha, los subárboles a partir de 2*i+1 y 2*i+2, en caso contrario (i >= nelementos), el árbol vacío.
- El árbol T, del conjunto de valores en la representación se aplica al árbol a partir de la posición 0.
Invariante de Representación
El invariante para un APO a es:
a.nelementos <= a.maxelementos.
a.vec apunta a un bloque de memoria reservada de a.maxelementos.
"i, j tal que 0 <= i < j < a.nelementos y (j = 2*i+1 o j = 2*i+2) a.vec[i] <= a.vec[j].
De manera que la clase APO en C++ tendría el siguiente aspecto:
Class APO
{
Public:
Apo ();
Apo (int tam);
Apo (const Apo<Tbase>& a);
Apo<Tbase>& operator = (const Apo<Tbase> &a);
const Tbase& minimo () const;
void borrar_minimo ();
void insertar (const Tbase& el);
void clear ();
int size () const;
bool empty () const;
~Apo ();
Private:
Tbase *vec;
int nelementos;
int maxelementos;
void expandir (int nelem);
}
Pasemos ahora a ver la implementación de cada una de las primitivas enunciadas con anterioridad en C++:
template <class Tbase>
Apo<Tbase>::Apo()
{
vec= new Tbase;
nelementos= 0;
maxelementos= 1;
}
template <class Tbase>
Apo<Tbase>::Apo(int tam)
{
vec= new Tbase[tam];
nelementos= 0;
maxelementos= tam;
}
template <class Tbase>
Apo<Tbase>::Apo (const Apo<Tbase>& a)
{
int i,aux;
aux=a.nelementos;
if (aux==0)
aux=1;
vec= new Tbase[aux];
nelementos= a.nelementos;
maxelementos= aux;
for (i=0;i<nelementos;i++)
vec[i]= a.vec[i];
}
template <class Tbase>
void Apo<Tbase>::expandir (int nelem)
{
Tbase *aux;
int i;
if (nelem > maxelementos)
{
aux= new Tbase[nelem];
for (i=0;i<nelementos;i++)
aux[i]=vec[i];
delete[] vec;
vec= aux;
maxelementos=nelem;
}
}
template <class Tbase>
Apo<Tbase>& Apo<Tbase>::operator = (const Apo<Tbase> &a)
{
int i;
if (this!=&a)
{
delete[] vec;
vec= new Tbase[a.nelementos];
nelementos= a.nelementos;
maxelementos= a.nelementos;
for (i=0;i<nelementos;i++)
vec[i]= a.vec[i];
}
return *this;
}
template <class Tbase>
inline const Tbase& Apo<Tbase>::minimo() const
{
assert(nelementos>0);
return vec[0];
}
template <class Tbase>
void Apo<Tbase>::borrar_minimo()
{
int pos,pos_min, ultimo;
bool acabar;
Tbase aux;
assert(nelementos>0);
vec[0]=vec[nelementos-1];
nelementos--;
if (nelementos>1)
{
ultimo= nelementos-1;
pos=0;
acabar= false;
while (pos<=(ultimo-1) / 2 && !acabar)
{
if (2*pos+1 == ultimo)
pos_min=2*pos+1;
else if (vec[2*pos+1] < vec[2*pos+2])
pos_min= 2*pos+1;
else pos_min= 2*pos+2;
if (vec[pos_min] < vec[pos])
{
aux= vec[pos];
vec[pos]=vec[pos_min];
vec[pos_min]= aux;
pos=pos_min;
}
else acabar= true;
}
}
}
template <class Tbase>
void Apo<Tbase>::insertar (const Tbase& el)
{
int pos;
Tbase aux;
if (nelementos==Maxelementos)
expandir(2*Maxelementos);
nelementos++;
pos=nelementos-1;
vec[pos]=el;
while ((pos>0) && (vec[pos]<vec[(pos-1)/2]))
{
aux= vec[pos];
vec[pos]=vec[(pos-1)/2];
vec[(pos-1)/2]= aux;
pos= (pos-1)/2;
}
}
template <class Tbase>
inline void Apo<Tbase>::clear()
{
nelementos=0;
}
template <class Tbase>
inline int Apo<Tbase>::size() const
{
return nelementos;
}
template <class Tbase>
inline bool Apo<Tbase>::empty() const
{
return nelementos==0;
}
template <class Tbase>
inline Apo<Tbase>::~Apo()
{
delete[] vec;
}
Para ejecutar el borrado de la raíz, no se puede quitar el nodo sin más ya que se desconectaria la estructura. Por otro lado si se quiere mantener la propiedad de orden parcial y el mayor balanceo posible con las hojas en el nivel más bajo alojadas de izquierda a derecha lo que podría hacerse es poner provisionalmente la hoja más a la derecha del nivel más bajo como raíz provisional, empujaremos entonces esta raíz hacia abajo intercambiándola con el hijo de etiqueta menor hasta que no podamos hacerlo más (porque sea ya una hoja o porque la etiqueta sea ya menor que la de cualquiera de sus hijos).
El anterior proceso aplicado a un árbol con n nodos toma un tiempo O(log2 n) puesto que en el árbol ningún camino tiene más de 1+log2 n nodos y el proceso de empujar hacia abajo intercambiando con los hijos toma un tiempo constante por nodo. En las siguientes figuras podemos observar este proceso sobre un ejemplo de borrado en un APO en el cual se elimina el nodo a para seguidamente subir a la raíz el nodo g que es empujado hacia abajo:
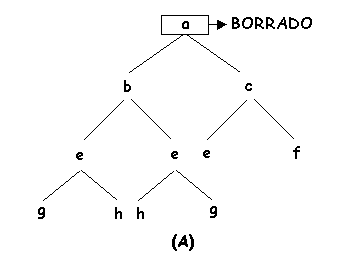

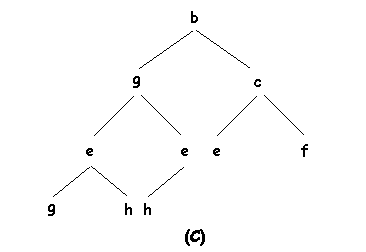
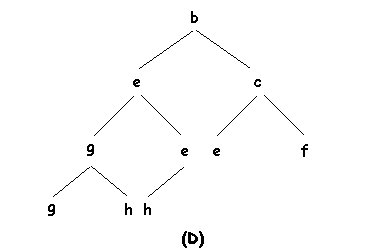
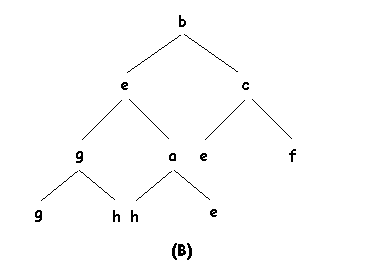
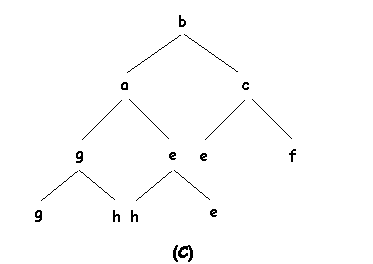
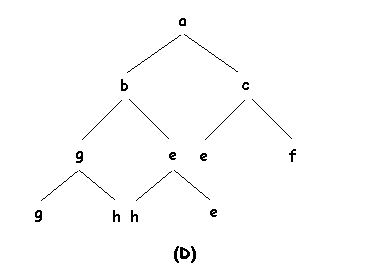
Para implementar la inserción habría que hacer unas consideraciones similares a las anteriores, el nuevo elemento que se inserta, lo podriamos situar provisionalmente en el nivel más bajo tan a la izquierda como sea posible (se comienza en un nuevo nivel si el último nivel está completo). A continuación se intercambia con su padre repitiéndose este proceso hasta que se cumpla la condición de orden parcial (bien porque ya esté en la raíz o porque tenga ya una etiqueta mayor que la de su padre).
Al igual que en el borrado puede verse fácilmente que este proceso no lleva más de O(log2 n) pasos. En las siguientes figuras podemos ver un ejemplo de inserción en un APO: