Introducción

Un árbol binario de búsqueda (ABB) es un árbol binario con la propiedad de que todos los elementos almacenados en el subárbol izquierdo de cualquier nodo x son menores que el elemento almacenado en x ,y todos los elementos almacenados en el subárbol derecho de x son mayores que el elemento almacenado en x.

 

La figura 1 muestra 2 ABB construidos en base al mismo conjunto de enteros:

 

 

 

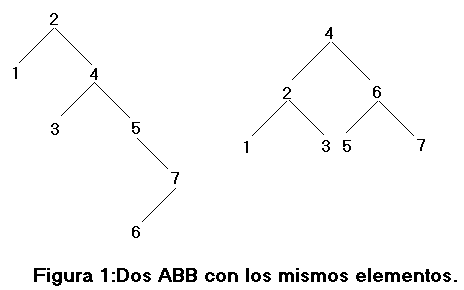
Obsérvese la interesante propiedad de que si se listan los nodos del ABB en inorden nos da la lista de nodos ordenada.Esta propiedad define un método de ordenación similar al Quicksort,con el nodo raíz jugando un papel similar al del elemento de partición del Quicksort aunque con los ABB hay un gasto extra de memoria mayor debido a los punteros.La propiedad de ABB hace que sea muy simple diseñar un procedimiento para realizar la búsqueda.:

 

Una instancia a del tipo de dato abstracto ABB sobre un dominio Tbase es un árbol binario con etiquetas en Tbase de manera que la etiqueta de un nodo es mayor que la de sus descendientes a la izquierda y menor que la de sus descendientes a la derecha. Para poder gestionarlo, debe existir la operación menor (<) para el tipo Tbase. Dos elementos base e1,e2 son iguales si no ((e1<e2) o (e2<e1)).

 

El espacio requerido para el almacenamiento es O(n). Donde n es el número de nodos del árbol.

 

 

 

Primitivas del árbol binario de búsqueda

 

Dentro del TDA ABB hemos propuesto las siguientes primitivas :

 

·        ABB ( ) -> constructor por defecto, reserva los recursos e inicializa el árbol a vacío.

 

·        ABB (const ABB<Tbase>& v) -> constructor de copia, construye el árbol duplicando el contenido de v en el árbol receptor.

PARÁMETROS : v -> ArbolBinario a copiar.

 

·        Void destruir (nodo *n) ->destruye el subárbol, libera los recursos que ocupa n y sus descendientes.

PARÁMETROS : n -> nodo que destruir junto con sus descendientes

             

·        Void copiar (nodo *&dest, nodo  orig) -> copia un subárbol, hace una copia de todo el  subárbol que cuelga de orig en el puntero dest. Es importante ver que en dest->padre (si existe) no se asigna ningún valor, pues no se conoce.

PARÁMETROS : dest -> referencia al puntero del que cuelga la copia.

                                  orig -> puntero a la raíz del subárbol a copiar.

 

·        Void enganchar (nodo *&r, nodo **m, int n) -> reconstruye un árbol equilibrándolo, reconstruye un árbol colgando en r, los n nodos que apunta la matriz m, asegurando que en la raíz de cada subárbol siempre se posiciona la mediana de los elementos a colgar. El subárbol obtenido está totalmente equilibrado.

PARÁMETROS : r -> puntero a la raíz del árbol a construir.

       m -> matriz con los punteros a los nodos.

                   n -> número de elementos en m, n > 1.

             

·        ABB<Tbase>& operator = (const ABB<Tbase> &v) ->asignación, asigna el valor del árbol duplicando el contenido de v en el árbol receptor. Devuelve la referencia al árbol receptor.

PARÁMETROS : v -> ABB a copiar.

 

·        Iterador primero () const -> inicia iterador, devuelve la posición del primer elemento, que coincide con la posición final si el árbol está vacío, el primer elemento es el más pequeño según la operación "<" del tipo Tbase.

 

·        Iterador siguiente (Iterador i) const -> iterador siguiente, el siguiente elemento corresponde al siguiente según la operación "<" del tipo Tbase.

PARÁMETROS : i -> iterador siguiente de i.

     

·        Iterador final () const -> iterador final, devuelve la posición final (detrás de la última), que coincide con la posición primera si el árbol está vacío.

 

·        Const Tbase& etiqueta (const Iterador n) const -> etiqueta indicada por el iterador, devuelve una referencia al elemento que indica el iterador n, es constante y por tanto no se puede modificar el valor.

PARÁMETROS : n -> iterador que indica el elemento, n no es final.

 

·        Iterador buscar (const Tbase& e) const -> búsqueda de elemento, devuelve el iterador que apunta a la posición del árbol donde se encuentra el elemento buscado e, si no se encuentra,

      devuelve la posición final, detrás de la última.

      PARÁMETROS : e -> etiqueta a buscar en el árbol receptor.

 

·        Bool insertar (const Tbase& e) -> inserción de un elemento, busca el elemento e en el árbol receptor, si lo encuentra lo reescribe de nuevo y devuelve false, si no, crea un nuevo nodo    en el árbol conteniéndo esta etiqueta y devuelve true.

      PARÁMETROS : e -> etiqueta a insertar en el árbol receptor.

 

·        Iterador borrar (const Iterador p) -> borrado en un elemento, borrar el elemento que se  almacena en el iterador p y devuelve el siguiente elemento a p por medio de un iterador.

PARÁMETROS : p -> iterador al elemento a borrar, no es final.

 

·        Void equilibrar () -> equilibra el árbol, equilibra el árbol binario de búsqueda receptor.

 

·        Void clear () -> borra todos los elementos, borra todos los elementos del árbol receptor., cuando termina, el árbol está vacío.

 

·        Int size () const -> número de elementos, devuelve el número de elementos del árbol receptor.

             

·        Bool empty () const -> vacío, devuelve true si el número de elementos del árbol  receptor es cero, false en otro caso.

             

·        Bool operator == (const ABB<Tbase>& v) const -> igualdad, devuelve true si el  árbol receptor tiene los mismos elementos  y en el mismo orden, false en caso contrario.

PARÁMETROS : v -> ABB con el que se desea comparar.

             

·        Bool operator != (const ABB<Tbase>& v) const -> distintos, devuelve true si el árbol receptor no tiene los mismos elementos y en el mismo orden, false en caso contrario.

PARÁMETROS : v -> ABB con el que se desea comparar.

             

·        ~ABB () -> destructor, libera los recursos ocupados por el árbol receptor.

Ejemplos de uso

 

Escribir ordenadamente los elementos de un ABB

 

Este programa lee de la entrada estándar un conjunto de enteros hasta el fin de entrada., después los lista todos, ordenados y sin repeticiones.

 

 #include <iostream>

 #include <ABB.h>

 

 int main (int argc, char *argv[])

    {

    ABB<int> a;

    ABB<int>::Iterador p;

    int i;

 

    while (cin>>i)

              a.insertar(i);

    for (p=a.primero();p!=a.final();p=a.siguiente(p))

          cout << a.etiqueta(p) << ' ';

    cout << endl;

    return 0;

   }

 

Escribir los elementos pares ordenadamente de un ABB

 

Este programa lee de la entrada estándar un conjunto de enteros hasta el fin de entrada, borra todos los elementos impares del conjunto y finalmente lista todos los pares, ordenados.

 

 #include <iostream>

 #include <ABB.h>

 

 int main (int argc, char *argv[])

    {

    ABB<int> a;

    ABB<int>::Iterador p;

    int i;

    while (cin>>i)

          a.insertar(i);

    for (p=a.primero();p!=a.final();)

          if (a.etiqueta(p)%2==1)

              p=a.borrar(p);

          else p=a.siguiente(p);

    for (p=a.primero();p!=a.final();p=a.siguiente(p))

          cout << a.etiqueta(p) << ' ';

    cout << endl;

    return 0;

    }

 

Implementación del ABB

 

Un ABB tiene los mismos componentes que un árbol binario, sólo que además del nodo raíz tenemos nelementos, que almacena el número de elementos del ABB y coincide con el número de nodos enlazados, veamos un ejemplo abajo:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

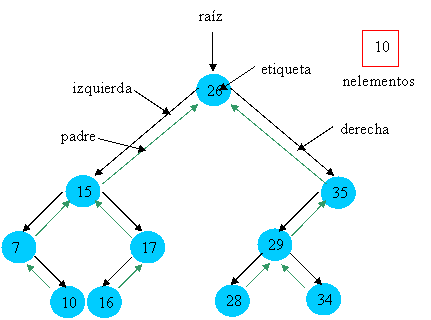
Vamos a ver la especificación tanto de la función de abstracción como del invariante de la representación del ABB:

 

 

Función de Abstracción

 

Sea T un árbol binario sobre el tipo Tbase, entonces si lo denotamos también Arbol (T.laraiz), es decir, como el árbol que cuelga de su raíz, entonces éste árbol del conjunto de valores en la representación se aplica al árbol:

 

{ T.laraiz -> etiqueta, {Arbol (T.laraiz -> izqda)}, {Arbol (T.laraiz -> drcha)}}

 

Donde { 0 } es el árbol vacío.

           

 

Invariante de Representación

 

Sea T, un árbol binario sobre el tipo Tbase, entonces el invariante de la representación es :

               

Si T es vacío, entonces T.laraiz = 0 y T.nelementos = 0, y si no:

 

T.laraiz -> padre =  0 y

 

"n nodo de T, n -> izqda ¹ n -> drcha y

 

"n, m nodos de T, si n -> izqda = m o n -> drcha = m entonces m ->padre = n y

 

"n, m nodos de T, si n -> izqda = m entonces n -> etiqueta > m -> etiqueta y

 

"n, m nodos de T, si n -> drcha = m entonces n -> etiqueta < m -> etiqueta y

 

T.nelementos = N (T.laraiz),donde N (n) = 1+ N (n -> izqda) + N (n -> drcha)  con N (0) = 0.

 

 

De manera que la clase ABB en C++ tendría el siguiente aspecto:

 

Class ABB

       {

       

       Public:

            typedef struct nodo *Iterador;

           

           ABB();

           ABB (const ABB<Tbase>& v);

           ABB<Tbase>& operator = (const ABB<Tbase> &v);

           Iterador primero() const;

           Iterador siguiente(Iterador i) const;

           Iterador final() const;

           const Tbase& etiqueta(const Iterador n) const;

           Iterador buscar(const Tbase& e) const;

           bool insertar(const Tbase& e);

           Iterador borrar(const Iterador p);

           void equilibrar();

           void clear();

           int size() const;

           bool empty() const;

           bool operator == (const ABB<Tbase>& v) const;

           bool operator != (const ABB<Tbase>& v) const;

           ~ABB();

    

    Private:

 

          struct nodo

              {

              Tbase etiqueta;

              struct nodo *izqda;

              struct nodo *drcha;

              struct nodo *padre;

              };

         

          struct nodo *laraiz;

          int nelementos;

 

          void destruir(nodo * n);

          void copiar(nodo *& dest, nodo * orig);

          void enganchar(nodo *&r, nodo **m, int n);

       }

 

 

Pasemos ahora a ver la implementación de cada una de las primitivas enunciadas con anterioridad en C++:

Por último vamos a hacer un par de comentarios referentes a las funciones insertar y borrar.

 

Puede probarse que una búsqueda o una inserción en un ABB requiere O(log₂n) operaciones en el caso medio,en un árbol construido a partir de n claves aleatorias, y en el peor caso una búsqueda en un ABB con n claves puede implicar revisar las n claves,o sea,es O(n).

 

Es evidente que si el elemento a borrar está en una hoja bastaría eliminarla,pero si el elemento está en un nodo interior, eliminándolo podríamos desconectar el árbol, para evitar que esto suceda se sigue el siguiente procedimiento:

 

·        Si el nodo a borrar u tiene sólo un hijo se sustituye u por ese hijo y el ABB quedará construido.

 

·        Si u tiene dos hijos,se encuentra el menor elemento de los descendientes del hijo derecho (o el mayor de los descendientes del hijo izquierdo) y se coloca en lugar de u,de forma que se continúe manteniendo la propiedad de ABB.