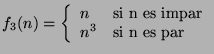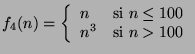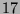 es
es 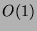
-
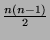 es
es 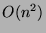 y
y 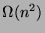 (es decir,
(es decir, 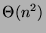 ).
).
-
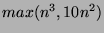 es
es 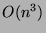
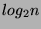 es
es
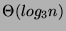
n,
- a.-
-
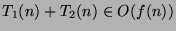
- b.-
-
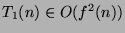
- c.-
-
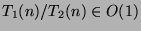
Indicar para cada par distinto ![]() y
y ![]() si
si ![]() es
es ![]() y si
y si
![]() es
es
![]() .
.
for (i=0;i<n;i++)
for (j=0;j<n;j++) {
C[i][j]= 0;
for (k=0;k<n;k++)
C[i][j]+=A[i][k]*B[k][j];
}
void ejemplo(int n)
{
int i, j, k;
for (i = 1; i < n; i++)
for (j = i+1; j <= n; j++)
for (k = 1; k <= j; k++)
Global += k*i;
}
for (i=0;i<n;i++)
if (i%2) {
for (j=i;j<n;j++)
x*=i;
for (j=1;j<i;j++)
y*=j;
}
void ejemplo(int n)
{
int x, cont;
cont = 0;
x = 2;
while (x < n)
{
x = 2*x;
cont++;
};
printf("%d\n", cont);
}
int recursiva(int n)
{
if (n <= 1)
return 1;
else
return (recursiva(n - 1) + recursiva(n - 1));
}
int E(int n)
{
if (n == 1)
return n;
else
return (E(n/2) + 1);
}
- >Cuál es el valor que devuelve la función?
- Obtener una expresión para el peor caso de tiempo de ejecución de la función.
- El máximo de la primera mitad.
- El máximo de la segunda mitad.
/* (cx,cy) son el centro del rect\'angulo y t es la longitud del lado del cuadrado */
/* rectangle (a,b,c,d) dibuja un rect\'angulo con esquina superior izqda (a,b) y esquina */
/* inferior derecha (c,d) */
void fractal (int n, int cx, int cy, int t)
{
if (n>0) {
rectangle(cx-t/2,cy-t/2,cx+t/2,cy+t/2);
fractal (n-1,cx-t/2,cy-t/2,t/4);
fractal (n-1,cx+t/2,cy+t/2,t/4);
fractal (n-1,cx-t/2,cy+t/2,t/4);
fractal (n-1,cx+t/2,cy-t/2,t/4);
}
}