REWIC WITH SELF-CONTROL


Table of Contents

Introduction

In absence of a priori knowledge about regions of interest, a rational system for progressive transmission chooses at any truncation time among alternative spatial orientation trees for further transmission in such a way as to avoid certain forms of behavioral inconsistency. Some rational transmission systems might exhibit aversion to risk involving ``gambles'' on tree-dependent quality of encoding while others favor taking such risks, but risk-prone systems as well as those with strong risk aversion appear not capable to attain the quality of reconstructions which can be achieved with moderate risk-averse behavior. Even though the problem of estimating the parameter that controls the risk attitude in a rational transmission system is a key issue, it is not clear how to pick the risk aversion parameter for different image content. A rational embedded wavelet image codec with self-control of quantizers' risk attitude integrates a rational progressive transmission system avoiding certain forms of behavioral inconsistency with an elementary form of cooperative bit allocation. In this scheme, self-control of quantizers' risk attitude provides an operational solution to the problem of risk attitude estimation at each truncation time. The following experimental results illustrate the comparative performance of the resultant scheme with both the state of the art in progressive transmission SPIHT and the state of art coder JPEG2000. Results were obtained without entropy-coding the bits put out with both SPIHT and REWIC with self-control.

Examples

The following examples show images encoded/decoded using (with entropy coding )JPEG 2000 (The JASPER Project Home Page.) and (without entropy coding) REWIC with self-control.The images are decomposed by a 6-level 9-7 tap biorthogonal Daubechies filter.

Experiments


A.Image Quality Predictor for Coder Performance Evaluation.

In the coding community the peak signal to noise ratio (PSNR) is used often to precisely measure and quantify the error present in a compressed image and great effort is expended toward minimizing such an error. Any coding scheme which does not attempt to minimize some square-error cannot be expected to prove their worth with a curve of PSNR versus bit rate ([1]), which may be a constraint on the formulation of new coding schemes capable of making an intelligent use of the visual information. This may be justified assuming the correctness of the PSNR, but what are the actual properties of the PSNR? For example, does it take into account of the effectiveness of the information, so discriminating relevant structures from unwanted detail and noise? Does it examine whether the properties of the original image at significant points are equal to the properties of the decoded output at the corresponding locations? The point is that whereas we have no evident affirmative answer to these and other questions, the PSNR does not appear capable of predicting visual distinctness from digital imagery as perceived by human observers  [2],[3],[4][5]

It often happens that the structure of a certain scene cannot be determined exactly due to various reasons (e.g, it is possible that some of the details may not be observable or the observer who makes an attempt to investigate the structure may no take all the relevant factors governing the structure into consideration). Under such circumstances, the structure of the reference image and the input image can be characterized statistically by discrete probability distributions. Let us assume the probabilities associated with the reference $R$ and the input $I$ as those given by $P$ and $Q$ . Then, the problem of predicting recognition times for humans performing visual search and detection tasks, can be reformulated as: What is the amount of relative information gain between the probability distributions $P$ and $Q$ ?

A number of postulates were proposed in [2] to characterize the information gain between two distributions with a minimal number of properties which are natural and thus desirable. For example a first postulate (Principle 1 [2] ) states a property of how unexpected a single event of a digital image was. A second postulate (Principle 2 $^{ \cite{garc:1}}$ ) was formulated to obtain a fair estimate of how unexpected a digital image was from some probability distribution by means of the mathematical expectation of how unexpected its single events were from this distribution. The Principle 3  [2] relates the estimate of how unexpected the reference image was from an ``estimated'' distribution and the estimate from the ``true'' distribution.

The human visual system does not process the image in a point-by-point manner but rather in a selective way according to the decisions made on a cognitive level, by choosing specific data on which to make judgments and weighting this data more heavily than the rest of the image, [6]. Hence, in order to devise measures that better capture the response of the human visual system, we should use a feature detection model for identifying significant locations at which to measure errors. This point is stated in Principle 4 [2].

We are interested in one approach in which the error between two images may be measured on locations of the reference picture at which humans might perceive some feature, for example, line features or step discontinuities. This point is stated in Principle 5 [2]. This postulate also presents the information conservation constraint: properties of the input image (e.g., first order local histograms) should be equal to the properties of the reference image at its significant locations.

The Principle 6  [2] states the significance conservation constraint, i.e. significance of interest points in the reference image is equal to the significance of the corresponding points in the input image. This constraint can help in qualitative comparison of the input image with the reference one.

From results in [2], we have that the compound gain (CG) between a test image $I$ and decoded outcome $O$ is a generalization of the Kullback-Leibler joint information gain of various random variables such that, it satisfies Postulates 1 through 6 in [2]:

\begin{displaymath} CG ( I, O) = \sum_{i=1}^{n} \sum_l p(I_{Z_i}) p(l / I_{Z_i})... ...g \frac{p(I_{Z_i}) p(l / I_{Z_i})}{p(O_{Z_i}) p(l / O_{Z_i})} \end{displaymath} (1)

with $Z_1, \cdots, Z_n$ being the significant locations of the test image $I$ ; $( p(l / I_{Z_i}) )_l $ being the local histogram computed on a neighborhood of location $Z_i$ in the test image $I$ ; $( p(l / O_{Z_i}) )_l $ being the local histogram computed on a neighborhood of $Z_i$ in the decoded outcome $O$ . In the above equation, $I_{Z_i}$ and $O_{Z_i}$ denote the events that the feature at location $Z_i$ is highly significant in order to explain the information content of the test image $I$ and the reconstruction $O$ , respectively; $p(I_{Z_i})$ and $p(O_{Z_i})$ being the a priori probabilities of occurrence of $I_{Z_i}$ and $O_{Z_i}$ , respectively.

Given any coding scheme the CG may then be applied to quantify the visual distinctness by means of the difference between the original image $I$ and decoded images at various bit rates. It allows us to analyze the behavior of coders from the viewpoint of the visual distinctness of their decoded outputs, taking into account that an optimal coder in this sense tends to produce the lowest value of the CG. The software and documentation of the compound gain may be accessed here. 
 


A.1 Experiment 1

A first experiment was designed to analyze the comparative performance of the PSNR and the CG for predicting visual (subjective) quality of reconstructed images using several compression methods.

To this aim, a test image was firstly compressed to the same bit rates using the state of the art in progressive transmission  SPIHT [7] (without entropy coding), the state of the art coder JPEG2000 [9], and REWIC with self-control (without entropy coding). This figure shows the respective reconstructed test images at 0.5, 0.25, and 0.125 bits per pixel (bpp).

Fifteen volunteers, nonexperts in image compression, subjectively evaluated the reconstructed images using an ITU-R Recommendation [10]. The ITU-R 500-10 recommends to classify the test pictures into five different quality groups:

SUBJECTIVE QUALITY FACTOR
5
 EXCELENT, The distortions are imperceptible
4
 GOOD, The distortions are perceptible
3
 FAIR, The distortions are slightly annoying
2
 POOR, The distortions are annoying
1
 BAD, The distortions are very annoying


  The method of assessment was cyclic in that the assessor was first presented with the original picture, then with the same picture but decoded at a bitrate. Following this she/he was asked to vote on the second one, keeping the original in mind. The assessor was presented with a series of pictures at different bitrates in random order to be assessed. At the end of the series of sessions, the mean score for each decoded picture was calculated. The next table  summarizes the mean quality factors for different decoded outputs using the compression methods.



bit/pixel
 MEAN QUALITY FACTOR
 
Rewic with self-control Jpeg2000 Spiht
0.5 4.67 4.67 4.60
0.25 3.80 2.80 2.93
0.125 3.00 1.73 1.61





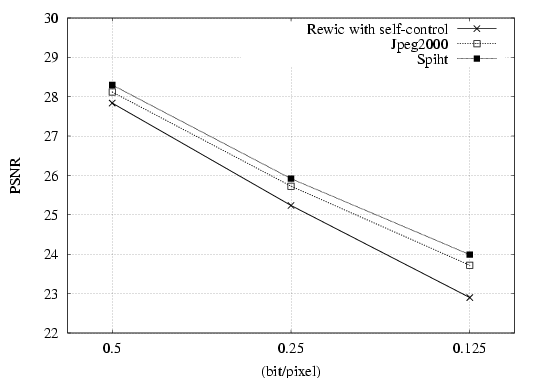
 2D plots on rate-distortion as given by the PSNR and the CG for REWIC with self-control, JPEG2000 and SPIHT at
0.5, 0.25, and 0.125 bpp.

 As can be seen from these figures, the PSNR predicts that the  SPIHT results in a higher image fidelity than both JPEG2000 and REWIC with self-control, which does not appear to correlate with subjective quality estimated by human observers (see table ). On the contrary, the overall impression is that, as predicted by the compound gain, the REWIC with self-control results in a higher image fidelity than SPIHT and JPEG2000 (recall that an optimal coder in this sense tends to produce the lowest value of the CG ), which correlates with subjective fidelity by humans. Also, the CG predicts a better visual fidelity using JPEG2000 than with the  SPIHT reconstructed images, which correlates with the subjective image quality in table.

A.2 Experiment 2

In this second experiment, a new test image was also compressed to the same bit rates using  SPIHT (without entropy coding), JPEG2000, and REWIC with self-control (without entropy coding). This figure shows the reconstructed test images at 0.5, 0.25, and 0.125 bpp. Again fifteen volunteers subjectively evaluated the reconstructed images as described above. The next summarizes the mean quality factors.



bit/pixel
 MEAN QUALITY FACTOR
 
Rewic with self-control   Jpeg2000  Spiht
0.5 3.33 2.87 2.33
0.25 2.27 1.27 1.27
0.125 1.10 1.00 1.00



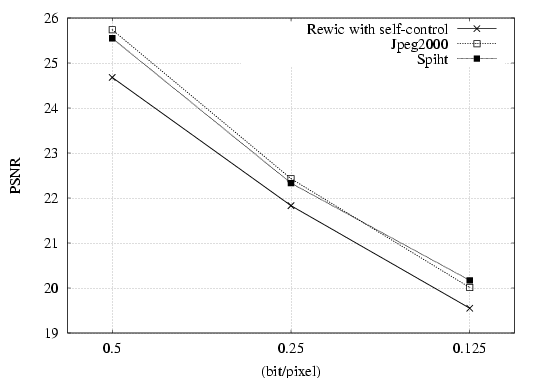
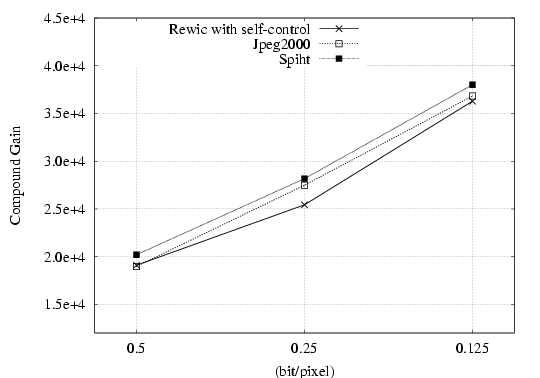
2D plots on rate-distortion as given by the PSNR and the CG for REWIC with self-control, JPEG2000 and SPIHT at
0.5, 0.25, and 0.125 bpp.

Up you can see 2D plots on rate-distortion as given by the PSNR and the CG for REWIC with self-control, JPEG2000 and SPIHT at 0.5, 0.25, and 0.125 bpp. For example, the PSNR predicts that both JPEG2000 and  SPIHT result in a higher image fidelity than REWIC with self-control, which does not appear to correlate with subjective quality estimated by human observers (see table ). On the contrary, as can be seen from  the figure, the compound gain predicts that REWIC with self-control results in a higher image fidelity than  SPIHT and JPEG2000, which correlates with subjective fidelity by humans given in the table. Summarizing, it seems that whereas the PSNR gives a poor measure of image quality, the CG is a good predictor of visual fidelity for humans performing subjective comparisons.


B.Coder Performance Evaluation


B.1 Experiment 3

Here we perform a thorough comparison of REWIC with self-control and  SPIHT, based on a the coder selection procedure presented in [11]. Results were obtained without entropy-coding the bits put out with both the REWIC with self-control and  SPIHT. Tests here reported were performed on a dataset composed of 49 standard $512 \times 512$ grayscale test images 

Given a test image $I$ , let $\{ I_{q(1)}^{spiht}, \cdots, I_{q(K)}^{spiht} \}$ be the set of decoded images at bitrates $q(1), \cdots, q(K)$ using  SPIHT; $\{ I_{q(1)}^{rewic}, \cdots, I_{q(K)}^{rewic} \}$ be the set of decoded images at bitrates $q(1), \cdots, q(K)$ using REWIC with self-control. The compound gain $CG $ may then be applied to quantify the visual distinctness by means of the difference between the original image $I$ and decoded images at various bit rates $q(i)$ :

\begin{displaymath} f(spiht, i) = CG ( I, I_{q(i)}^{spiht} ) \, . \end{displaymath} (2)

and similarly, $f(rewic,i)$ .

Once distortion functions $f(\dag , i)$ have been calculated following equation (2), we make use of an objective criterion for coder selection based on the overall difference between the two functions $f(spiht, i)$ and $f(rewic,i)$ , which can be measured by a Kolmogorov-Smirnov (K-S) test to a certain required level of significance.

Definition: Coder Selection Procedure. In the language of statistical hypothesis testing, the coding scheme $REWIC$ with self-control is significantly better than $SPIHT$ for the test image $I$ if the following two conditions are true:

(1)
$f(rewic, i) \leq f(spiht, i)$ , with $i = 1,2, \cdots, K$ ; and
(2)
we disprove, to a certain required level of significance, the null hypothesis of a Kolmogorov-Smirnov test that two sets $\{ f(rewic, i) \mid i = 1,2, \cdots, K \}$ and $\{ f(spiht, i) \mid i = 1,2, \cdots, K \}$ are drawn from the same population distribution function.

Condition 1 takes into account that an optimal coder tends to produce the lowest value of $f( \dag , i$ across bit rates, and disproving the null hypothesis in condition 2 in effect proves data sets $\{ f(rewic, i) \mid i = 1,2, \cdots, K \}$ and $\{ f(spiht, i) \mid i = 1,2, \cdots, K \}$ are from different distributions. If both conditions hold, it allows us to assess the fact that, for the test image, $\{ f(rewic, i) \mid i = 1,2, \cdots, K \}$ is significantly better than $\{ f(spiht, i) \mid i = 1,2, \cdots, K \}$ .



CODER SELECTION PROCEDURE WITH % CONFIDENCE (REWIC with self-control against SPIHT)
      Condition 1 Condition 2           
IMAGES  (y/n ) (-/y/n ) Confidence 
$\begin{array}{c} \char93 1, \char93 2, \char93 3, \char93 4, \char93 14, \... ...42, \char93 43, \char93 44, \char93 46, \char93 47, \char93 49 \end{array}$ $y$ $y$ 99 %
# 5, # 13, # 39, # 45, # 48  $y$ $y$ 95 %
# 31 $y$ $n$ $-$
$\begin{array}{c} \char93 6, \char93 7, \char93 8, \char93 9, \char93 10, \char93 11, \char93 12, \char93 17, \char93 18 \end{array}$ $n$ $-$ $-$


The last table  summarizes the results of this experiment on the test images of the dataset : Thirty-nine out of forty-nine test images (79 %) have passed conditions (1) and (2) in the coder selection procedure, and hence, the REWIC with self-control is significantly better than  SPIHT with high confidence level for seventy-nine percent of test images.


B.2 Experiment 4

REWIC with self-control results from the integration of a rational embedded wavelet codec (called REWIC in [11]) with the cooperative action for bit allocation--called COllective Rationality for the ALlocation of bits [12] (CORAL). Hence, the REWIC with self-control should improve the performance of REWIC with a fixed risk attitude in order to achieve the performance levels of the CORAL scheme while still maintaining the embedded property. To analyze this point, we test in this fourth experiment the comparative performance of REWIC  [11] with risk aversion parameter $r$ set to $0$ , REWIC with self-control and CORAL [12]  against SPIHT [7]. Results were obtained without entropy-coding the bits put out with the coding schemes.

To this aim we employ again the coder selection procedure as described above. The next table  illustrates the three comparative performances on the dataset of 49 test images. As can be seen from this table: (i) REWIC with risk aversion parameter $r$ set to $0$ is significantly better than SPIHT with high confidence level for sixty-one percent of test images; (2)CORAL is significantly better than SPIHT with high confidence level for seventy-four percent of test images; and (3) as we know from the previous experiment, REWIC with self-control is significantly better than SPIHT with high confidence level for seventy-nine percent of images.



PERCENTAGE OF IMAGES AT WHICH REWIC/CORAL ARE
SIGNIFICANTLY BETTER THAN SPIHT AT LEAST WITH 90 % CONFIDENCE
REWIC (r=0) better than SPIHT 61 %
REWIC with self-control better than SPIHT 79 %
CORAL better than SPIHT 74 %


We also compare the performance in rate-distortion sense of the REWIC with risk aversion parameter set to 0, REWIC with self-control, and CORAL, where the distortion is the compound gain .
To illustrate more clearly the results of the comparison,  for the dataset of 49  images, in this figure  shows the respective 2D plots on rate-distortion as given by the CG for the three coding schemes. The compression ratio ranges from 128:1 to 16:1.



B.3 Experiment 5

In a last experiment we test the comparative performance of the state of the art coder JPEG2000 [8], using the Jasper [9] implementation, against the state of the art in progressive transmission SPIHT and the REWIC with self-control. Results were obtained without entropy-coding the bits put out with SPIHT and REWIC with self-control. Again the coder selection procedure was used to this aim. The next table illustrates the comparative performance on the dataset of 49 test images. As can be seen from this table: (i) JPEG2000 is significantly better than SPIHT with high confidence level for sixty-three percent of test images; and (2) JPEG2000 is significantly better than REWIC with self-control with high confidence level for zero percent of test images.

PERCENTAGE OF IMAGES AT WHICH JPEG2000 IS SIGNIFICANTLY
BETTER THAN SPIHT/REWIC AT LEAST WITH 90 % CONFIDENCE
JPEG2000 better than SPIHT 63 %
JPEG2000 better than REWIC with self-control 0 %


This comparison can be also given from a different point of view just comparing SPIHT/REWIC against JPEG2000. The results are given in the next table: SPIHT is better than JPEG2000 for zero percent of images, whereas REWIC with self-control is better than  JPEG2000 for fourteen percent of images.



PERCENTAGE OF IMAGES AT WHICH SPIHT/REWIC ARE
SIGNIFICANTLY BETTER THAN JPEG2000 AT LEAST WITH 90 % CONFIDENCE
SPIHT better than JPEG2000 0 %
REWIC with self-control better than JPEG2000 14 %


This figure illustrates the performance in a rate-CG sense of the  JPEG2000 , SPIHT, and REWIC with self-control on  the dataset of 49 test images . 

Bibliography

1

D. Schilling and P. Cosman, ``Image Quality Evaluation based on Recognition Times for Fast Image Browsing Applications,'' IEEE Transactions on Multimedia, 4(3), pp. 320-331, (2002).

2
J.A. Garcia, J. Fdez-Valdivia, Xose R. Fdez-Vidal, and Rosa Rodriguez-Sanchez, ``Information Theoretic Measure for Visual Target Distinctness,'' IEEE Trans. on Pattern Analysis and Machine Intelligence, 23(4), 362-383, (2001).

3
J.A. Garcia, J. Fdez-Valdivia, X.R. Fdez-Vidal, and R. Rodriguez-Sanchez, Computational models for predicting visual target distinctness, SPIE Optical Engineering Press, Bellingham, Washington USA, Vol. PM95, (2001).

4
A. Toet, P. Bijl, J.M. Valeton, ``Image dataset for testing search and detection models,'' Optical Engineering, 40(9), pp. 1756-1759, (2001).

5
X.R. Fdez-Vidal, A. Toet, J.A. Garcia, J. Fdez-Valdivia, ``Computing visual target distinctness through selective filtering, statistical features, and visual patterns,'' Optical Engineering, 39(1), 267-281, (2000).

6
Pashler, H. Attention. Psychology Press, (1998).
7
         A.Said, and W.A. Pearlman, "A new, fast and efficient image codec based on set partitioning in hierarchical trees," IEEE Trans. on Circuit and System for          Video Technology, Vol 6, No. 3 pp. 243-250, (1996)
8
C. Christopoulos (editor), ``JPEG2000 verification model 5.0 (technical description),'' ISO/IEC JTC1/SC29/WG1 N1420, August (1999).

9
M.D. Adams, and F. Kossentini, ``Jasper: A software-based JPEG-2000 codec implementation'', Procc. IEEE International Conference on Image Processing, Vancouver BC, Canada, October (2000).

10
ITU-R Recommendations, Broadcasting service (television): Recommendation 500-10, Supplement 3 to Volume 1997, BT Series, 2000 Edition.
11   
          J.A. García, Rosa Rodríguez-Sanchez, J. Fdez-Valdivia, and Xose R. Fdez-Vidal, "Rational systems exhibit moderate risk aversion with respect to "gambles"          on variable-resolution compression." Optical Engineering. Vol 41, No. 9 pp. 2216-2237. (2002)     
12
         J.A. García, Rosa Rodríguez-Sanchez, J. Fdez-Valdivia, and Xose R. Fdez-Vidal, "CORAL: Collective rationality for the allocation of bits." Optical          Engineering Vol.  42, No 4, April ( 2003)