COMPOUND GAIN: A visual distinctness metric for coder performance evaluation
Table of Contents
- Introduction
- Directory Structure and Building the Software
- Using the Software
- Experiments
- Reporting Bugs
- Copyright
Introduction
Various distinctness metrics have been proposed to compare and rank target detectability, and to quantify background or scene complexity. As a matter of fact it is of great practical value to have computational visual differences or distinctness measures which can be applied to evaluate image displays, (virtual) scene generators, image compression methods, image reproduction methods, camouflage measures, and traffic safety devices. Relevant computational models of early human vision typically process an input image through various bandpass filters and analyze first order statistical properties of the filtered images to compute a target distinctness metric. If they give good predictors of target saliency for humans performing visual search and detection tasks, they may be used to compute visual distinctness of image subregions (target areas) from digital imagery.
Target saliency for humans performing visual search and detection tasks can be estimated by the difference between the signal from the target-and-background scene and the signal from the background with no target. It often happens that the structure of a certain scene cannot be determined exactly due to various reasons (e.g, it is possible that some of the details may not be observable or the observer who makes an attempt to investigate the structure may no take all the relevant factors governing the structure into consideration). Under such circumstances, the structure of the reference image and the input image can be characterized statistically by discrete probability distributions. Then, since the certain relationship such that greater visual distinctness implies lesser recognition response times, the problem of predicting recognition times for humans performing visual search and detection tasks, can be reformulated as: What is the amount of relative information gain between the respective probability distributions?
A
generalization of the Kullback-Leibler joint information gain of various
random variables (called as compound gain) is a measure of information
gain between two images such that, it satisfies a series of postulates
which are natural and thus desirable ("Information
theoretic measure for visual target distinctness" J.A. García,
J. Fdez-Valdivia, X.R. Fdez-Vidal, Rosa Rodriguez-Sánchez. IEEE
Trans. on Pattern Analysis and Machine Intelligence, vol. 23 (4) pp. 362-383.
(2001)).
The form of the compound gain (CG) between a test image I and decoded O outcome is:
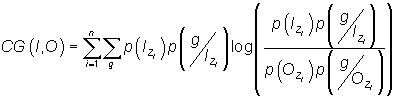
with
 being the significant locations
of the test image I;
g denotes the grey level;
being the significant locations
of the test image I;
g denotes the grey level;  being the local histogram computed on a neighborhood of location
being the local histogram computed on a neighborhood of location 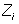 in the test image I;
in the test image I;
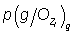 being the local histogram
computed on a neighborhood
being the local histogram
computed on a neighborhood 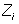 of in the decoded outcome O. In the above equation,
of in the decoded outcome O. In the above equation, 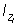 and
and 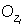 denote the events that
the feature at location
denote the events that
the feature at location 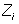 is highly significant in order to explain the information content of the
test I image
and the reconstruction O, respectively;
is highly significant in order to explain the information content of the
test I image
and the reconstruction O, respectively; 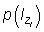 and
and 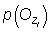 being the a priori probabilities
of occurrence of
being the a priori probabilities
of occurrence of 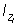 and
and 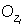 ,
respectively.
,
respectively.
Given any coding scheme the CG may then be applied to quantify the visual distinctness by means of the difference between the original image and decoded images at various bit rates. It allows us to analyze the behavior of coders from the viewpoint of the visual distinctness of their decoded outputs, taking into account that an optimal coder in this sense tends to produce the lowest value of the CG.
From
results in ("Information theoretic
measure for visual target distinctness" J.A. García, J. Fdez-Valdivia,
X.R. Fdez-Vidal, Rosa Rodriguez-Sánchez. IEEE Trans. on Pattern
Analysis and Machine Intelligence, vol. 23 (4) pp. 362-383. (2001))
we can conclude that the compound gain appears to relate to visual target
distinctness as perceived by human observers. This result implies that
the CG can be used to predict visual distinctness of targets in complex
backgrounds from digital imagery. This finding may eliminate the need
for psychophysical experiments, which are time consuming, and sometimes
even impossible to perform.
This research was sponsored by the Spanish Board for
Science and Technology, (CICYT) under grant TIC2000-1421
.
Directory Structure and Building the Software
For getting and uncompressing the tar do:
- gunzip cg.tar.gz
-
tar xvf cg.tar
- src: contains the source files, including the file "Makefile" to generate the executables
- bin_linux: contains one executable file for a linux platform
- example: contains test data
The CGerror software is intended to be built using the file "Makefile".
Using the Software
The CGerror software consists only in one program:CGerror.out . The executable program.
The CGerror Command
Synopsis
CGerror.out <Original_image> <Input_image>Description
CGerror.out The program obtain the Compund Gain error beetwen two images.Parameters
The CGerror.out program needs the following parameters:
NOTE: don't introduce in the command line the extention ".pgm"Output
The output is the Compund Gain measure and this number is put in the file CGerror.dat.
Usage
The next sentence shows how to use the command CGerror.out on the test.pgm image ( a 512x512 graylevel pgm image) and its compressed version at 0.16 bpp (test_0.16.pgm):
> CGerror.out test test_0.16
NOTE: These images have been included in the example directory inside the gziped tarfile.
Experiments
Experiment 1:
This experiment was designed to analyze the comparative performance of the PSNR and the CG for predicting visual (subjective) quality of reconstructed images using several compression methods.
To this aim, a test image was firstly compressed to the same bit rates using the SPIHT, JPEG2000, REWIC (without entropy coding), and CORAL (without entropy coding).
In the next figures (click here), show the respective reconstructed test images at 0.5, 0.25, and 0.16 bits per pixel (bpp).
Thirteen volunteers, nonexperts in image compression, subjectively evaluated the reconstructed images using an ITU-R Recommendation ("Broadcasting service (television) Recommendation 500-10". Supplement 3, vol 1997. BT series 2000 edition). The ITU-R 500-10 recommends to classify the test pictures into five different quality groups:
SUBJECTIVE
QUALITY FACTOR |
|
5 |
EXCELENT, The distortions are imperceptible |
4 |
GOOD, The distortions are perceptible |
3 |
FAIR, The distortions are slightly annoying |
2 |
POOR, The distortions are annoying |
| 1 |
BAD, The distortions are very annoying |
The method of assessment was cyclic in that the assessor was first presented with the original picture, then with the same picture but decoded at a bitrate. Following this he was asked to vote on the second one, keeping the original in mind. The assessor was presented with a series of pictures at different bitrates in random order to be assessed. At the end of the series of sessions, the mean score for each decoded picture was calculated. The next table summarizes the mean quality factors for different decoded outputs using the compression methods (data in graphical format).
bit/pixel |
MEAN
QUALITY FACTOR |
|||
Coral |
Rewic |
Jpeg2000 |
Spiht |
|
0.5 |
3.45 |
3.38 |
2.84 |
2.62 |
0.25 |
2.31 |
2.69 |
1.61 |
2 |
0.16 |
1.61 |
1.31 |
1.61 |
1.61 |
MEAN |
2.46 |
2.46 |
2.02 |
1.98 |
The next figures (click here) show 2D plots on rate-distortion as given by the PSNR and the CG for CORAL, REWIC, JPEG200 and SPIHT at 0.5, 0.25, and 0.16 bpp.
Summarizing, it seems that whereas the PSNR gives a poor measure of image quality, the CG is a good predictor of visual fidelity for humans performing subjective comparisons. For example, the PSNR predicts that the SPIHT results in a higher image fidelity than both CORAL and REWIC, which does not appear to correlate with subjective quality estimated by human observers. On the contrary, the overall impression is that, as predicted by the compound gain, the CORAL and REWIC schemes result in a higher image fidelity than SPIHT, which correlates with subjective fidelity by humans. Also, the CG predicts a better visual fidelity using CORAL than with the JPEG2000 reconstructed image at 0.5 and 0.25 bpp, which correlates with the subjective image quality measured by human beings, although the JPEG2000 gives a better PSNR performance than CORAL at the same bit rates. As said before, since the CORAL and REWIC do not attempt to minimize MSE, cannot be expected to prove its worth with a curve of PSNR versus bit rate.
Experiment 2: Comparative performance of the CG-rate curves for the JPEG2000, CORAL, SPIHT, and REWIC coding algorithms
In
this section we compare the performance in rate-distortion sense of
the JPEG2000, CORAL, SPIHT, and REWIC, where
the distortion is the compound gain (CG).
Results were obtained without entropy-coding the bits put out with
the CORAL, REWIC, and SPIHT schemes. Test here reported were performed
on a dataset composed of 49 standard 512x512 grayscale
test images.
The elicitation of the optimal coding scheme consists of calculating
the visual distinctness by means of the compound gain between a test
image I and images reconstructed under various
degrees of lossy compression. It allows us to analyze the behavior
of coders, taking into account that an optimal coder tends to produce
the lowest value of the compound gain.
The result of the comparison ( CG curves for every test image) show the respective 2D plots on rate-distortion as given by the CG for JPEG2000, CORAL, SPIHT, and REWIC. The compression ratio ranges from 64:1 to 16:1. The CORAL, SPIHT, and REWIC were not improved by entropy-coding their outputs, and thus, the bitstreams put out are binary uncoded (without entropy coding)."
These 2D plots show that: (i) The JPEG2000
gives a better CG performance than CORAL, REWIC,
and SPIHT, for six test images
(i.e., #1, #6, #11, #13, #22, #24) ; (ii) for
test image #30, the REWIC
gives the best CG performance of the four methods;
(iii) the CORAL gives
a better CG performance than JPEG2000, REWIC, SPIHT
for twenty-seven test images
(i.e., #3, #4, #5, #7, #9, #14, #16, #17, #20, #25, #26, #27, #28,
#29, #31, #32, #34, #35, #36, #37, #41, #42, #43, #45, #46, #47, #49);
and (iv) both JPEG2000 and CORAL
give the best CG performance for fifteen
images (i.e., #2, #8, #10, #12, #15, #18,#19,#21,#23,#33,#38,#39,#40,#44,#48).
Reporting Bugs
- The details of the run-time system (i.e., operating system)
- The compiler that you are using.
- The command line options used when the problem was observed.
- Indicate whether or not the problem is reproducible, and if the problem is reproducible, indicate the exact steps required to reproduce the problem.
Copyright
This
site last update (dd/mm/yy) : |
Members
| Research lines
| Research projects
| Publications |
Software | Links © 2002-03. Computer Vision Group. University of Granada |